How to Find the Eigenvalues: The Hidden Power Behind Matrix Mathematics

Eigenvalues—those nearly invisible numbers that govern the behavior of linear transformations—lie at the core of modern mathematics, physics, and engineering. Though they appear in dense equations and abstract theory, eigenvalues underlie crucial applications like structural analysis, quantum mechanics, and data science. Understanding how to compute them transforms abstract matrices into powerful tools capable of modeling complex systems.

This article reveals a step-by-step approach to finding eigenvalues with precision, clarity, and practical insight—for anyone ready to decode the mathematical forces shaping technology and science.

Understanding Eigenvalues: More Than Just Numbers

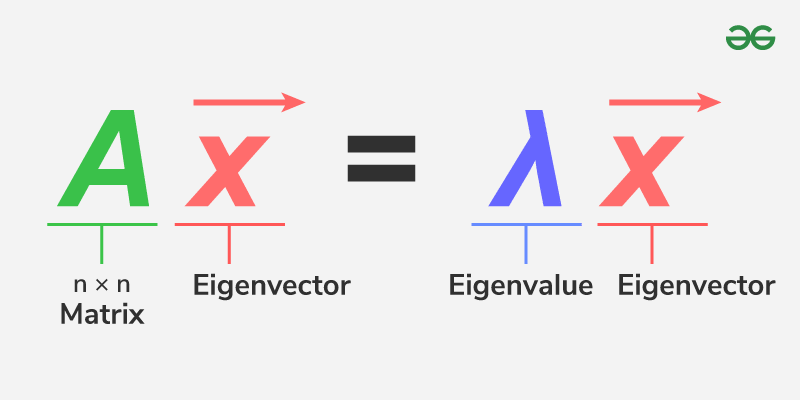
An eigenvalue is a scalar that reveals how a linear transformation stretches or compresses vector spaces along specific directions—called eigenvectors. In matrix terms, for a square matrix \( A \), an eigenvalue \( \lambda \) satisfies the defining equation:

\( A\mathbf{v} = \lambda\mathbf{v} \)

where \( \mathbf{v} \) is a non-zero vector (the eigenvector). This equation signifies that multiplying \( A \) by \( \mathbf{v} \) scales \( \mathbf{v} \) without changing its direction.

Eigenvalues thus identify stable states, modal frequencies, and energy levels in physical systems. “Eigenvalues are the fingerprints of matrices,” notes mathematician Dr. Elena Ruiz, “each revealing something fundamental about the matrix’s geometric and algebraic nature.”

Step-by-Step: How to Solve for Eigenvalues

Finding eigenvalues involves a structured sequence of linear algebra techniques.

While computational tools now handle much of the heavy lifting, grasping the underlying process is essential for deep understanding and effective application. Below are the core methods used in both theoretical and applied contexts:

• Characteristic Equation Method: The Foundational Approach
• Begin by forming the characteristic polynomial: \( \det(A - \lambda I) = 0 \), where \( A - \lambda I \) is the matrix \( A \) minus \( \lambda \) times the identity matrix. This determinant, a function of \( \lambda \), forms an \( n \times n \) polynomial.

  Solve for \( \lambda \) by setting this polynomial equal to zero.

• For small matrices, expanding the determinant by cofactor expansion is feasible. For larger systems, symbolic algebra software simplifies this step, but understanding expansion via minors forms the conceptual bedrock.
• Example: For a 2×2 matrix \( A = \begin{bmatrix} 3 & 1 \\ 1 & 3 \end{bmatrix} \), \( A - \lambda I = \begin{bmatrix} 3 - \lambda & 1 \\ 1 & 3 - \lambda \end{bmatrix} \) The determinant is: \( (3 - \lambda)^2 - 1 = \lambda^2 - 6\lambda + 8 = 0 \) Roots are \( \lambda = 4 \) and \( \lambda = 2 \)—eigenvalues revealing maximum and minimum transformation effects.
1. Numerical Methods: When Exact Solutions Fail
2. High-dimensional or complex matrices often resist analytical eigenvalue derivation. In such cases, numerical algorithms become indispensable.

   The most widely used is the **QR Algorithm**, which iteratively decomposes a matrix into a quasi-special form to converge on eigenvalues.

3. Software applications like MATLAB, NumPy, and R implement these algorithms efficiently, but knowing the iterative logic—such as Gershgorin’s Circle Theorem for approximations or Rayleigh quotient refinements—enhances interpretation and error management.
4. Applications Deriving from Eigenvalues: - In quantum mechanics, eigenvalues correspond to measurable energy levels. - In vibration analysis, they determine natural frequencies of mechanical structures. - In machine learning, eigenvalues quantify data variance via Principal Component Analysis (PCA), enabling dimensionality reduction.

The transition from equation to insight hinges on choosing the right method—symbolic for elegance, numerical for scale—while anchoring results in context.

Advanced Techniques and Refinements

For larger or sparse matrices, refinements improve accuracy and efficiency.

Iterative methods like the **Power Iteration** and **Inverse Iteration** focus computational effort on dominant eigenvalues, useful in large-scale simulations. For symmetric matrices—common in statistics and physics—eigenvalues are guaranteed real and orthogonal eigenvectors simplify orthogonal diagonalization, a powerful technique to decompose matrix operations:

If \( A \) is symmetric (\( A = A^T \)), it can be expressed as \( A = Q\Lambda Q^T \), where \( Q \) contains orthogonal eigenvectors and \( \Lambda \) holds real eigenvalues. This decomposition powers methods like PCA and stability analysis, ensuring robust results.

Practical Tools and Software for Eigenvalue Computation

Modern practitioners rely on software to perform eigenvalue calculations with precision and speed.

Key tools include:

• Python (NumPy, SciPy): The `numpy.linalg.eig()` function computes eigenvalues and eigenvectors efficiently, supporting dense matrices and sparse inputs.
• MATLAB: Offers `eig()` with built-in support for complex matrices and iterative solvers, widely used in engineering and physics.
• Mathematica & Maple: Symbolic engines allow exact eigenvalue computation, ideal for small matrices and pedagogical use.
• Specialized Libraries: StoLPACK and ARPACK enable high-performance eigenvalue solves for large sparse systems used in simulations and big data analytics.

Common Pitfalls and How to Avoid Them

Despite available tools, errors in eigenvalue computation persist. Common issues include:

• Neglecting Matrix Size Constraints: Eigenvalue algorithms assume square matrices; non-square inputs yield undefined determinants. Verify \( A \) is square before proceeding.
• Ignoring Numerical Stability: Ill-conditioned matrices amplify rounding errors.

  Use condition number checks and iterative refinement to improve accuracy.

• Misinterpreting Convergence: Iterative methods may fail to converge. Monitor residual norms and apply fallback algorithms when necessary.
• Overlooking Complex Eigenvalues: Real matrices often yield complex eigenvalues—neglecting these in sensitive applications (e.g., oscillatory systems) risks flawed modeling.

Balancing computer power with manual insight prevents missteps and ensures reliable outcomes.

The Power of Eigenvalues in Action

From predicting quantum behavior to stabilizing skyscrapers, eigenvalues empower disciplines across science and engineering. They distill complex transformations into interpretable numbers, revealing hidden regularities in chaos.

“Understanding eigenvalues is not just about solving equations—it’s about seeing the architecture of systems,” says Dr. Ruiz. “Once grasped, these values unlock modeling, optimization, and innovation across fields.” Whether used directly via code or interpreted through theory, eigenvalues remain one of mathematics’ most influential and accessible concepts—bridging abstraction and real-world impact with clarity and precision.

The journey to find eigenvalues reveals not just a formula, but a framework: from characteristic polynomials to numerical iteration, each step reinforces a deep connection between algebra and reality. As technology evolves, so too does the capacity to harness eigenvalues—transforming matrices into tools that shape the technologies shaping our future.