Mastering Rational Numbers: Definitions, Examples, and Their Role in Everyday Mathematics

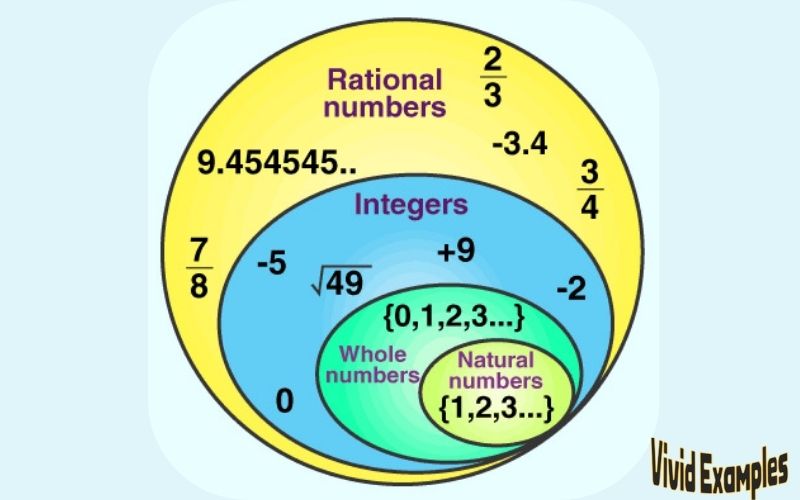
Defining rational numbers with precision reveals a foundational pillar of mathematics—numbers that express part-whole relationships through ratios of integers. A rational number, formally defined as any number that can be written as the quotient \( \frac{p}{q} \), where \( p \) and \( q \) are integers and \( q \neq 0 \), forms a countably infinite set that underpins arithmetic, algebra, and real-world measurement. These numbers bridge whole numbers and more abstract real values, enabling precise representation of quantities such as fractions, repeating decimals, and terminating decimals.

At the core of rational numbers lies the principle of expressibility: every rational number corresponds uniquely to a fraction derived from two integers. For instance, \( \frac{3}{4} \), \( -\frac{5}{2} \), and \( \frac{7}{1} \) all qualify, illustrating the variety of valid forms. The numerator \( p \) represents how many parts are considered, while the non-zero denominator \( q \) specifies the size of each part.

This structure ensures clarity and consistency across calculations. Rational numbers encompass an extensive set defined by both finite and infinite decimal expansions. Terminating decimals, such as \( 0.75 = \frac{3}{4} \), can be expressed exactly in fractional form.

Similarly, repeating decimals—like \( 0.\overline{3} = \frac{1}{3} \)—highlight a deeper connection between rationality and recurring digit patterns. Importantly, not all decimals are rational; numbers like \( \sqrt{2} \) or \( \pi \) (which are irrational) cannot be written as a ratio of integers, reinforcing the definitional boundary rational numbers occupy in number theory. Examples illustrate their broad utility.

Consider daily use: dividing a pizza into 8 slices and consuming 3 leaves \( \frac{3}{8} \) consumed—exactly a rational fraction. Or calculating a sale discount: a 25% discount on \$80 equals $ 0.25 \times 80 = 20 $, where 0.25 is the rational decimal \( \frac{1}{4} \). These practical instances confirm rational numbers are not abstract constructs but essential tools for precise decision-making.

Mathematically, properties of rational numbers follow logically from their definition. The set is closed under addition, subtraction, multiplication, and division (except by zero), meaning operations involving rational numbers consistently yield rational results. For example: \[ \frac{1}{2} + \frac{1}{3} = \frac{5}{6}, \quad \frac{3}{4} \times \frac{2}{5} = \frac{6}{20} = \frac{3}{10} \] Yet, rational numbers possess special density: between any two distinct rationals, infinitely many others exist.

This density supports calculus and real analysis, where rational approximations refine continuity and convergence. Computational handling of rational numbers demands care. In algebra and programming, representing quantities as fractions avoids floating-point rounding errors common with decimals.

For instance, balancing equations in chemistry or calculating precise interest rates in finance requires exact rational arithmetic. Modern calculators and computer systems often encode rational values as special floating-point variants or symbolic expressions to preserve accuracy. Children’s mathematics education frequently introduces rational numbers through visual models.

Pie charts, number lines, and fraction bars translate abstract definitions into tangible understanding. Students learn early that \( \frac{1}{2} \) of a whole is unmistakably more than half but less than whole—precisely where rationality provides clarity. Global standards and curricula emphasize rational numbers as a gateway to numerical reasoning.

From primary school arithmetic to advanced algebra, understanding rational forms enables learners to interpret equations, solve proportions, and manipulate variables with confidence. Goals include fluency with adding, subtracting, multiplying, and dividing fractions, alongside recognizing equivalent forms—critical skills in standardized testing and real-world problem-solving. A deeper insight lies in the elegance of rational number structure.

Every rational fraction \( \frac{p}{q} \) corresponds to a point on the Cartesian number line, with repeating decimals revealing cyclical patterns intrinsic to division. This geometric interpretation reinforces their logical consistency and visual stability across representations. Quantitatively, the set of rational numbers is infinite yet countable—a first infinite set proven by Cantor, where each fraction can be enumerated in a sequence.

This set density contrasts sharply with the uncountable reals, underscoring rationals’ density yet limited cardinality within the continuum of real numbers. In applied mathematics, rational numbers enable exact modeling where precision matters. Engineering tolerances, architectural blueprints, and scientific measurements rely on rational data to ensure consistency and accuracy.

For example, electrical resistance expressed in ohms often reduces to simple fractions when Ohm’s Law involves current and voltage ratios like \( \frac{10}{3} \) ohms. Many misconceptions surround rational numbers. A common error assumes all decimals are rational—false for non-terminating, non-repeating variations.

Others assume only whole numbers are valid, overlooking that \( \frac{1}{2} \) is rational and foundational in scaling. Correcting these reinforces precise arithmetic expectations. Ultimately, rational numbers form a mathematically rigorous, universally accessible, and profoundly useful set.

Their definition—fractional ratios of integers—unlocks clarity in computation, depth in theory, and reliability in application. From classroom lessons to professional calculations, rational numbers remain indispensable. Understanding rational numbers through precise definition and diverse examples reveals their central role in mathematics and daily life.

Their structure supports logical reasoning, accurate measurement, and enduring numerical fluency—proving that even the simplest ratios hold profound significance in both abstract thought and practical reality.

Rational numbers, defined as fractions of integers with non-zero denominators, are indispensable in mathematics: they enable precise representation of parts, repeating decimals, and exact computation. Their definition ensures clarity in arithmetic and algebra, while their density across the number line supports advanced analysis.

From dividing a cake to calculating interest, rational numbers bridge theory and real-world application with unmatched accuracy.

Examples such as \( \frac{2}{5} \) (part of a whole), \( 0.\overline{6} \) (equivalent to \( \frac{2}{3} \)), and \( -\frac{3}{4} \) show rational numbers adapt to whole, finite, and infinite patterns. They form a countably infinite set closed under standard operations, with density that supports rigorous mathematical exploration. In education, these numbers anchor conceptual understanding, preparing learners to navigate proportional reasoning and symbolic manipulation.

In applied contexts, rational numbers provide exactness critical to science, finance, and engineering.

Their structured form avoids approximation errors, ensuring reproducible results. While reals contain all possibilities, rationals offer a practical, predictable subset that balances completeness and usability. Because every rational number emerges from two integers, they embody logic at its purest, forming the backbone of quantitative precision.

Thus, rational numbers—defined as ratios of integers—stand as a cornerstone of mathematical literacy.

Their definition, examples, and real-world integration reveal not only their theoretical elegance but also their indispensable role in both elementary arithmetic and advanced scientific inquiry. Mastery of rational numbers empowers clear thinking, precise computation, and confidence in an increasingly data-driven world.