Mastering Right Triangles and Trigonometry: The Core of Algebraic Thinking

The intricate dance between right triangles and trigonometry lies at the heart of All Things Algebra, serving as both a foundational pillar and a powerful gateway to advanced mathematical understanding. From solving real-world problems to unlocking college-level applications, the principles governing right triangles and trigonometric functions are indispensable tools for students and professionals alike. Gina Wilson’s approach to these concepts elegantly bridges abstract algebra with geometric intuition, transforming complex ideas into accessible, actionable knowledge.

With a clear structure, practical examples, and proven techniques, her methods illuminate why right triangles remain a cornerstone of mathematical education.

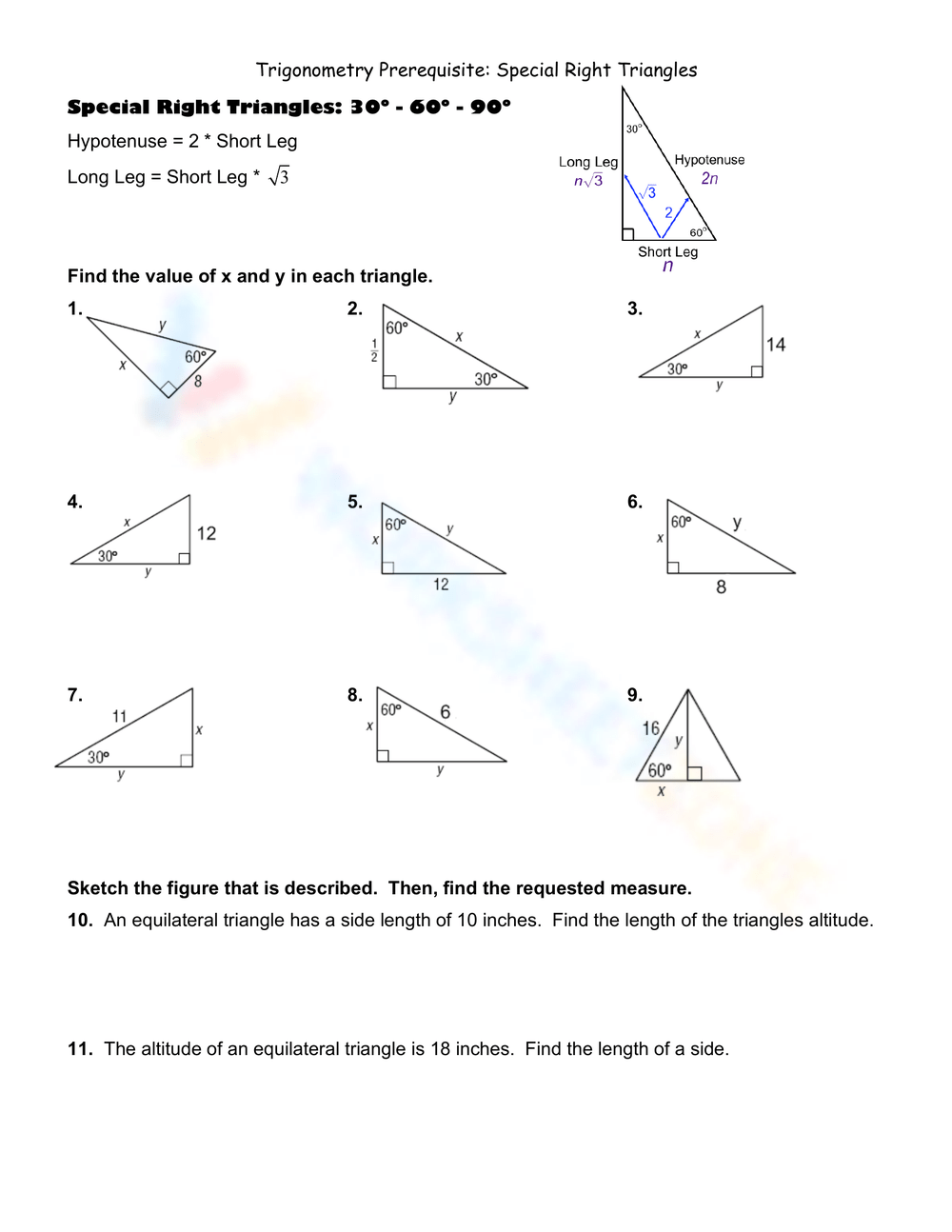
Right triangles, defined by having one 90-degree angle, offer a simple yet profoundly powerful framework. The relationships between their sides and angles form the basis of trigonometric ratios—sine, cosine, and tangent—each defined through ratios of precise segments.

These ratios are not arbitrary: they form consistent, predictable relationships that allow for exact calculation and inference. Understanding these ratios is essential, as they underpin everything from surveying and architecture to physics and engineering.

The Essential Trigonometric Ratios: Definition and Use

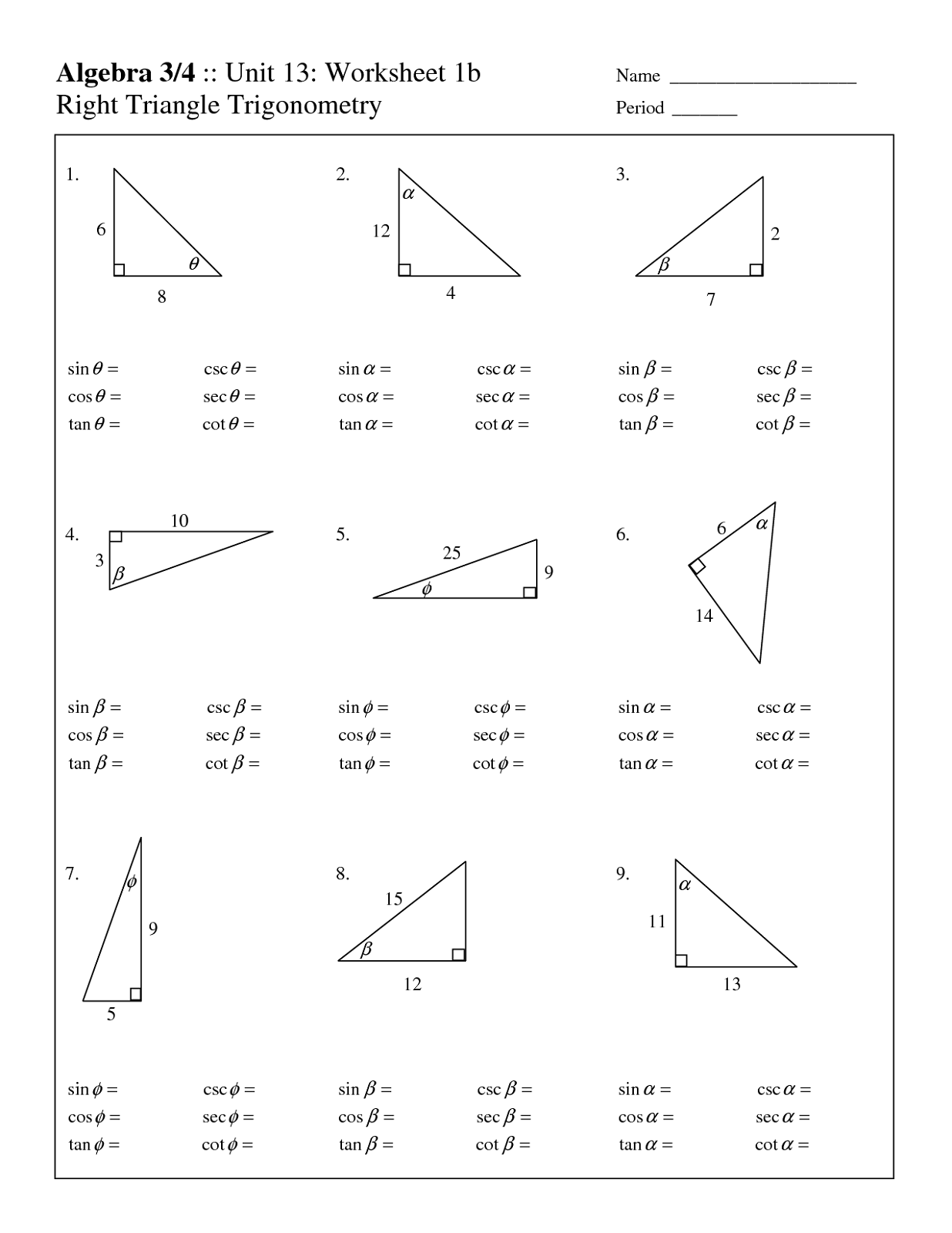
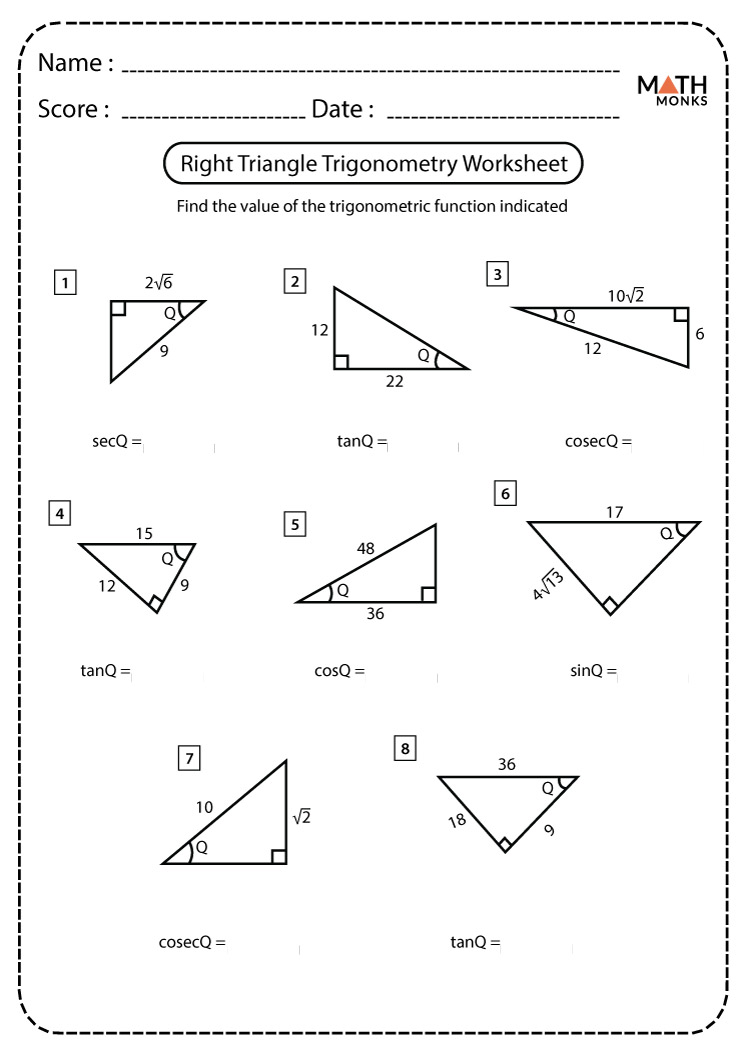
The three primary trigonometric functions—sine (sin), cosine (cos), and tangent (tan)—are defined based on the lengths of sides in a right triangle relative to one of its acute angles: - **Sine (sin)** = opposite / hypotenuse - **Cosine (cos)** = adjacent / hypotenuse - **Tangent (tan)** = opposite / adjacent For Gina Wilson, clarity begins with defining these ratios not as isolated formulas but as relational tools that reflect real proportions.

“Every angle tells a story about the shape of the triangle,” Wilson emphasizes in her instructional materials. “Knowing which sides correspond to sine, cosine, and tangent transforms abstract concepts into tangible geometry.” These ratios remain constant for a given angle, regardless of the triangle’s size—a property known as angular equivalence. This constancy enables students to solve for unknowns in problem sets with confidence.

For example, if a surveyor measures the 30° angle between a ladder and the ground and knows the ladder’s perpendicular reach (opposite side), they can compute the distance to the base using tan(30°) = opposite / adjacent.

Mastering the ratios requires more than memorization—it demands active understanding through multiple representations: numerical substitution, graphical interpretation, and real-world application. Visual learners benefit from unit circle diagrams, where sine and cosine values correspond to coordinates on a circle of radius one, reinforcing their periodic nature.

Algebraic problem-solving sharpens precision, as rearranging the basic identity sin²θ + cos²θ = 1 unlocks solutions in identity proofs and optimization problems.

Applications That Matter: From Everyday Problems to Professional Practice

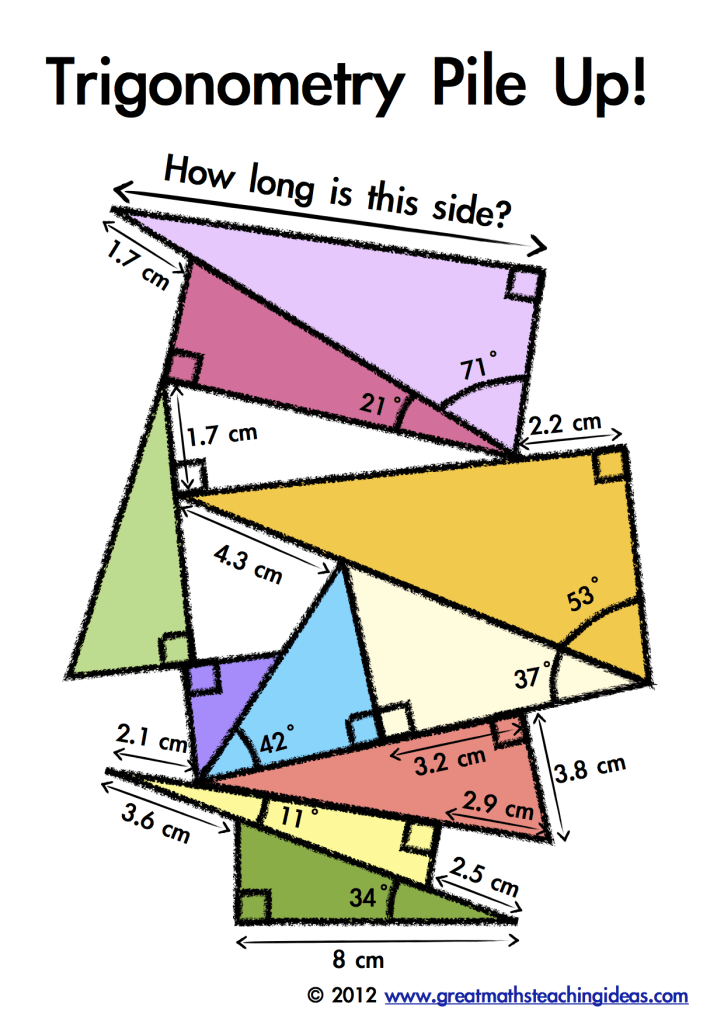
The true power of right triangles and trigonometry emerges when applied beyond the classroom. In construction, these principles ensure structural integrity—calculating roof slopes, determining beam angles, and verifying roof pitch angles prevent costly errors.

Architects rely on trigonometric scaling to translate plans into physical space, ensuring geometric harmony across blueprints and built environments. In navigation, trigonometry enables accurate pathfinding. Previously known as “dead reckoning,” modern GPS systems still depend on angle and distance computations rooted in right triangle relationships.

For adventurers and sailors, understanding trigonometric functions aids in triangulating positions using visible landmarks or signals. Physics and engineering extend this utility further. Mechanical systems depend on angular motion calculations; electrical engineers use phase angles derived from trigonometric functions to analyze alternating currents.

Even computer graphics—rendering realistic 3D models—leverage right triangle ratios to project perspective and depth, bringing virtual worlds to life.

These applications reveal that functional fluency with right triangles and trigonometry is not merely academic—it is a gateway to problem-solving mastery across disciplines. Whether designing bridges or mapping flight trajectories, trigonometric precision underpins modern innovation.

Education experts note that early, intuitive encounters with right triangles lay the groundwork for abstract reasoning in higher math and science, making Wilson’s materials a strategic choice for students at every level.

The Pedagogical Edge: How Gina Wilson Teaches Right Triangles

Gina Wilson’s approach distinguishes itself through clarity, consistency, and real-world relevance. She structures lessons so students first visualize right triangles, identify angles and side labels with precision, then apply sine, cosine, and tangent through guided practice.

“I avoid overwhelming students with too many formulas at once,” Wilson explains. “Instead, I build confidence step by step—starting with basic ratios, then moving to identities, and finally to applications.” Her methods integrate seamlessly with algebraic thinking. Students learn to express trigonometric values algebraically, substitute variables, and manipulate equations—skills directly transferable to solving equations, modeling relationships, and analyzing functions.

This fusion of algebra and geometry fosters deeper reasoning, enabling learners to see math not as a collection of procedures, but as a coherent, interconnected system.

Key instructional strategies include:

• Side labeling practices:
Complex figures often challenge students to identify triangles within larger designs. Wilson’s consistent labeling conventions reduce confusion and reinforce pattern recognition.
• Contextual problem sets:
Real-life scenarios—such as calculating heights of buildings from shadow lengths or determining distances across rivers—anchor abstract ratios in tangible experiences.
• Error analysis:
Students learn to verify solutions by returning to foundational ratios, fostering deeper conceptual understanding and reducing mechanical memorization.

By anchoring trigonometry in geometry and algebra, Wilson’s methods cultivate not just computation skills but a holistic mathematical mindset—one essential for students preparing for standardized tests, college STEM programs, and careers requiring analytical rigor.

As mathematics evolves, so too does its visual language—trigonometric principles remain constant constants. The relationship between right triangles and trigonometric functions continues to empower learners to decode spatial relationships, model real-world phenomena, and innovate beyond the page. With guided clarity and practical application, Gina Wilson’s approach to right triangles and trigonometry doesn’t just teach formulas—it builds mathematical intuition, the kind needed to excel in an increasingly quantitative world.

For anyone seeking to master this foundational domain, her resources stand as both compass and catalyst, turning confusion into confidence and equations into insight.