Ordered Pair Definition: The Mathematical Foundation of Modern Logic and Structured Data

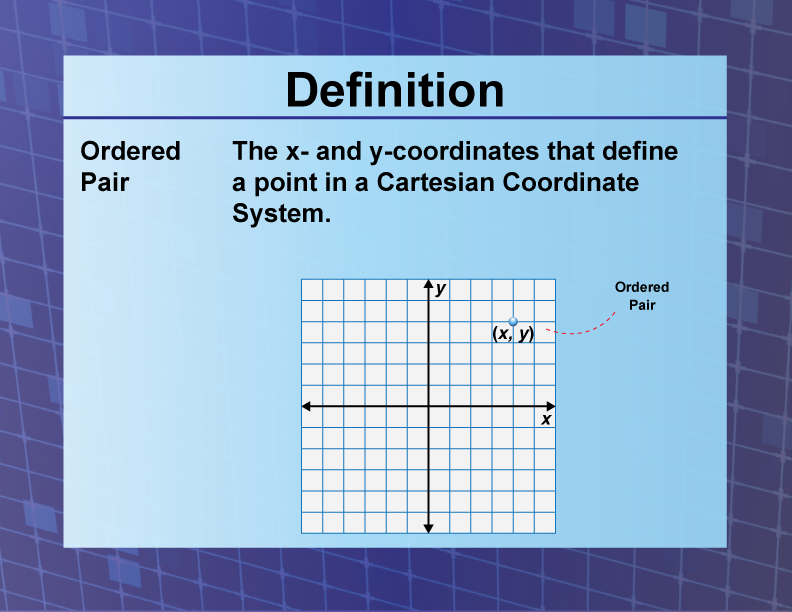
An ordered pair, formally defined as a collection of two elements where position determines meaning, stands as one of the most foundational building blocks in mathematics, computer science, and formal logic. Defined formally as the set \((a, b) = \{ \{a\}, \{a, b\} \}\), this definition ensures that the sequence of elements is preserved and that \((a, b) \neq (b, a)\) unless \(a = b\). More than a mere notation, the ordered pair underpins critical concepts across disciplines—from Cartesian coordinates to database relationships.

Its clarity and precision make it indispensable for representing comm ordered relationships, enabling unambiguous expression in both theoretical and applied domains.

The Formal Definition and Historical Roots of Ordered Pairs

The modern definition of an ordered pair emerged from set theory, pioneered in the late 19th century by Georg Cantor, but it was Ernst Zermelo in 1904 who formally introduced the set-theoretic construction that defines \((a, b)\) as the unique set containing \(a\) and \(b\) with structural distinction between members. This definition satisfies a key logical requirement: order matters. While unordered pairs such as \(\{a, b\}\) treat elements as interchangeable, ordered pairs enforce distinction—making \((3, 5)\ fundamentally different from \((5, 3)\).

This distinction ensures that relationships like function mapping, coordinate geometry, and relational database keys remain unambiguous. The formal elegance of this construct lies in its simplicity: two elements structured into a single, precise entity.

Ordered Pairs in Cartesian Geometry and Coordinate Systems

One of the most pervasive applications of the ordered pair definition is in defining points in two- and three-dimensional space. A point \((x, y)\) in the plane is precisely a location determined by its x-coordinate followed by its y-coordinate—each coordinate position dictating location with mathematical rigor.

Extending this, points in three-dimensional space are denoted \((x, y, z)\), preserving order and enabling precise spatial representation. This system, foundational to graphing functions, solving geometric problems, and modeling physical phenomena, relies entirely on the ordered pair’s structural integrity. “The coordinate system is impossible without ordered pairs,” observes mathematician Dr.

Lena Cho, “they transform abstract values into tangible spatial relationships.”

Ordered Pairs and Function Representation

Functions, defined as mappings from inputs to outputs, are inherently structured through ordered pairs. A function \(f\) is formally a subset of the Cartesian product \(A \times B\)—where each ordered pair \((a, b)\) signifies \(a\) maps to \(b\). Unlike arbitrary relations, functions require uniqueness and no repeated outputs for a single input, which the ordered pair enforces.

For example, the function mapping water temperature to states (solid, liquid, gas) captures each input-output pair gas reperation uniquely. This precision prevents ambiguity: \((20^\circ C, \text{liquid})\) is distinct from \((20^\circ C, \text{freezing point})\), a nuance critical in scientific and computational contexts. “Without ordered pairs, the term ‘function’ loses its mathematical precision,” notes statistician Alex Rivera, “each pair is a statement of defined correspondence.”

Applications in Databases and Information Systems

Beyond geometry and functions, ordered pairs serve as the backbone of relational databases.

In SQL and other systems, primary and foreign keys rely on ordered pairs to establish relationships between tables. For example, a customer (identified by \((cust\_id, name)\)) linking to an order \(((cust\_id, order\_id))\) ensures referential integrity. This structure allows queries to retrieve precise, linked data—essential for reporting, analytics, and data consistency.

The ordered pair’s definition guarantees that each link maintains uniqueness: \((101, 50)\) identifies one customer-order pair, never two. “In the age of big data, ordered pairs organize complexity with mathematical rigor,” explains database architect Elena Torres, “they ensure every piece of information knows exactly where it belongs.”

Ordered Pairs and Advanced Logic and Relations

The utility of ordered pairs extends into abstract logic and mathematics, where they define relations as sets of ordered pairs. A binary relation \(R\) on sets \(A\) and \(B\) is a collection of \((a, b)\) such that \(a \in A\) and \(b \in B\), with \((a, b) \in R\) indicating association.

This formulation underpins equality, implication, and complex logical expressions. For instance, the proposition “if \(x\) is a parent of \(y\), then \(y\) is a child of \(x\)” is modeled as an ordered pair relationship reversed and bid