Planck’s Constant in Electron Volt: The Quantum Yardstick That Powers Modern Science
Planck’s Constant in Electron Volt: The Quantum Yardstick That Powers Modern Science
A single number—Planck’s constant, denoted as *h*—forms the bedrock of quantum physics, serving as the indispensable bridge between energy and frequency in the subatomic world. When expressed in electron volts (eV), this fundamental constant becomes the lingua franca of atomic and particle physics, enabling precise measurement and calculation of energy at the quantum scale. At 6.62607015×10⁻³⁴ joule-seconds, Planck’s constant governs the discrete nature of energy exchange, revealing how radiation and matter interact at the most fundamental level.
This relationship, encapsulated in Einstein’s iconic equation *E = hf*, defines how a photon’s energy depends on its frequency—a principle that underpins everything from laser spectroscopy to quantum computing. By anchoring energy measurements to electron volts, scientists transform abstract quantum behavior into real-world applications with tangible precision. The adoption of electron volts as the standard energy unit in particle and atomic physics has streamlined research across disciplines.
Defined as the energy gained (or lost) by a single electron moving through a voltage difference of one volt, the electron volt (1 eV = 1.602×10⁻¹⁹ joules) offers an intuitive scale for expressing energies relevant to electrons and other subatomic particles. When converted using Planck’s constant, the frequency of emitted or absorbed radiation reveals its quantized nature, making *h eV* not just a unit, but a physical descriptor of energy transitions in atoms, molecules, and devices. High-precision instruments from mass spectrometers to semiconductor detectors rely on this conversion to resolve energy differences with remarkable sensitivity.
Quantifying the Quantum: How Planck’s Constant Bridges Frequency and Energy
The relationship between frequency and energy, governed by Planck’s constant, is the cornerstone of quantum theory. Each photon’s energy is directly proportional to its oscillation speed—frequency—multiplied by *h*. This quantum link—*E = hf*—was revolutionized by Einstein’s 1905 explanation of the photoelectric effect, where he demonstrated that light delivers energy in discrete packets whose size depends on frequency.“The emission and absorption of energy occur in precise quanta,” as physicist Richard Feynman once noted, “and the size of each quantum is set by Planck’s constant.” At the core of this principle is the electron volt, a unit uniquely suited to quantum phenomena. When scientists measure the frequency of electromagnetic waves reflecting off an atom, like in spectroscopy, converting that frequency into energy requires *h*. For example, a photon with a frequency of 10¹⁵ hertz carries energy of roughly 12.3 eV, a value derived directly from *E = hf*.
With precise values of *h* (6.62607015×10⁻³⁴ J·s) and *e* (1.602×10⁻¹⁹ C), *E in eV = (hf)/e*, enabling consistent, reproducible energy measurements across experiments and instruments. This synergy ensures global collaboration in fields ranging from quantum optics to materials science.
Applications Across Technology and Fundamental Science
Planck’s constant in electron volts fuels countless technological and scientific advances.In semiconductor physics, the concept underpins bandgap engineering, where the minimum energy needed to excite a silicon electron (typically ~1.1 eV) dictates device efficiency in solar cells and LEDs. Using *h eV*, researchers calculate electronic transitions critical to optoelectronic applications. In nuclear and particle physics, the eV-planck framework enables precise energy budgeting.
A positron-electron annihilation releases energy equivalent to 1.022 MeV—two electrons each contributing 0.511 MeV, a direct sum rooted in quantum conservation laws expressed via *h*. This energy precision guides detector design and collision analysis in large facilities like CERN’s Large Hadron Collider (LHC), where minute energy shifts reveal new particles and interactions. Spectroscopy, a cornerstone of analytical chemistry and astronomy, also relies heavily on this pairing.
Techniques such as X-ray photoelectron spectroscopy (XPS) use *h eV* conversions to map electron binding energies, exposing elemental composition and chemical states with atomic-level resolution. Similarly, astrophysical observations decode stellar spectra by translating emitted light frequencies into energy levels measurable in electron volts. Quantum computing and quantum cryptography further illustrate the practical power of *h eV*.
In qubit operation, energy differences of a few millielectron volts define state transitions critical to superposition and entanglement. Experiments tuning superconducting circuits or trapped ions rely on *h eV* precision to maintain coherence and fidelity. “Without Planck’s constant, we could not quantify the miniscule energy scales that enable quantum technologies,” observes Dr.
Elena Marquez, a quantum researcher at the Institute for Advanced Quantum Studies. 

.webp)
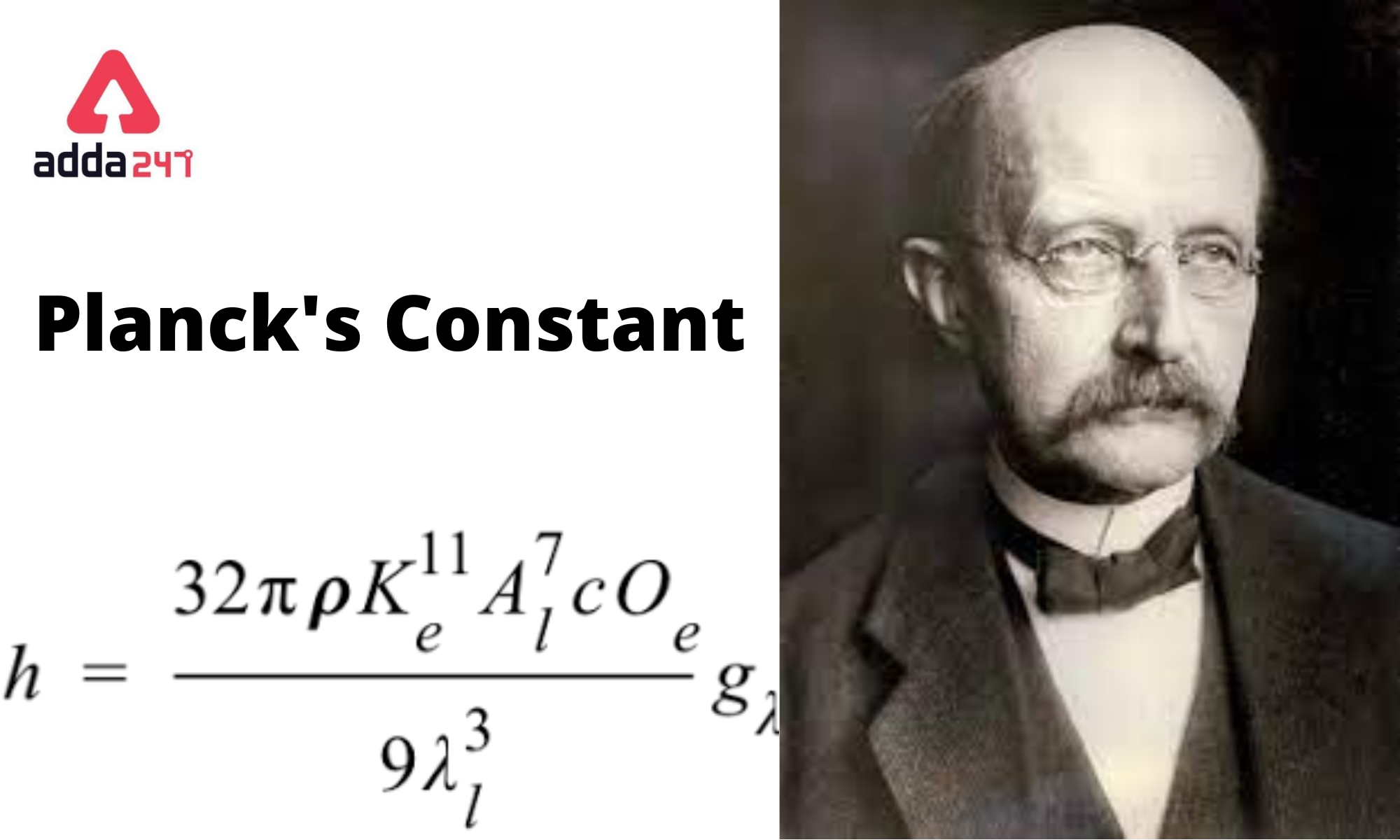
Related Post

¿CCcam Ha Muerto? El Fin de un Ícono del Hacking en 2024 y las Alternativas Emergentes

Unlock Hidden Power: The Street Smart Chinese Magic Sentences Toolkit PDF Transforms Language Mastery

Yandy Smith: From Dynamic Beginnings to Stardom—A Multifaceted Career Built on Resilience, Rep with Status, and Strategic Partnerships

Kasper Kansas: The Quiet Architect Behind a Modern Powerhouse of Sustainable Innovation

