Revealing the Power of Change in Log: How Base Transformation Drives Data Insight
Revealing the Power of Change in Log: How Base Transformation Drives Data Insight
In the fast-evolving world of digital data, understanding how information evolves over time is not just valuable—it’s essential. Base Change In Log emerges as a transformative mathematical tool in log analysis, enabling experts to detect, model, and interpret structural shifts in data sequences with remarkable precision. By translating complex changes through logarithmic scaling and base transformations, analysts unlock hidden patterns in time series, user behavior, and system performance that conventional methods often miss.
Why Logs Matter – and Why Change Counts Logarithms are foundational in data science, especially when analyzing phenomena that span orders of magnitude—such as user growth, financial transactions, or signal strength. Unlike linear scales, logarithmic transformations compress extremes, revealing nuanced trends across vast datasets. But raw logs, while mathematically convenient, rarely tell the full story.
That’s where Base Change In Log comes in: a strategic shift in base values and logarithmic framing that illuminates how rates of change evolve, offering deeper diagnostic power.
The Mechanics of Base Change in Log
At its core, Base Change In Log refers to the deliberate transformation of logarithmic representations by altering the base—shifting from natural logs (base *e*), base 10, or custom bases—without losing analytical integrity. This change doesn’t distort data but reinterprets its rate of progression relative to a new reference frame.For example, converting from log₁₀ to log₂ alters how multiplicative growth is perceived, effectively rescaling the magnitude of change per unit time. This mathematical agility allows analysts to: - Normalize disparate datasets with different scaling units, enabling direct comparison. - Detect subtle inflection points where growth accelerates or decelerates across different basises.
- Stabilize variance in non-linear systems, improving model accuracy and forecast reliability. “Base change in log isn’t just a notation shift—it’s a lens that reshapes perspective,” says Dr. Elena Torres, a data systems specialist at the Global Analytics Institute.
“By adjusting the base, we recalibrate how we interpret growth rates, revealing dynamics invisible in standard logarithmic scales.”
Practical Applications Across Industries
The real-world value of Base Change In Log surfaces across disciplines where dynamic data unfolds continuously. **Finance and Market Trends** In algorithmic trading and risk modeling, base-transformed logs help detect shifts in volatility or momentum that standard models overlook. For instance, transforming daily return logs from base 10 to base 2 can highlight logarithmic accelerate-ups in asset volatility, flagging potential market regime changes earlier.Traders using these refined signals gain sharper edge, detecting inflection points just before major price moves. **Technology and User Analytics** Tech platforms leverage base-change techniques to interpret logarithmic user engagement curves—critical for feature rollout success or churn prediction. A sudden flattening in log-scaled retention curves, analyzed across bases like base 2 and base 3, signals changes in user stickiness that linear logs fail to capture.
“User drop-offs often unfold logarithmically, but their inflection points vary wildly depending on base,” explains Rajiv Mehta, senior data engineer at a leading SaaS provider. “Base change transforms noisy signals into actionable insights, empowering proactive product decisions.” **Environmental and Scientific Monitoring** Climate scientists use base-transformed logs to track long-term temperature shifts and emission trajectories across decades. By switching logarithmic bases, researchers identify non-linear accelerations in carbon concentrations or glacial melt rates, improving the calibration of climate models and policy impact projections.
Best Practices in Implementing Base Transformations
To harness Base Change In Log effectively, practitioners must observe key principles: - **Match Base to Scope**: Base 2 excels in binary growth (exponential adoptions), base 10 suits imperial or metric scale compatibility, while non-standard bases adapt to domain-specific rhythms. - **Preserve Relationships**: Transformations must maintain statistical integrity—ensuring ratios and proportional changes remain consistent across bases.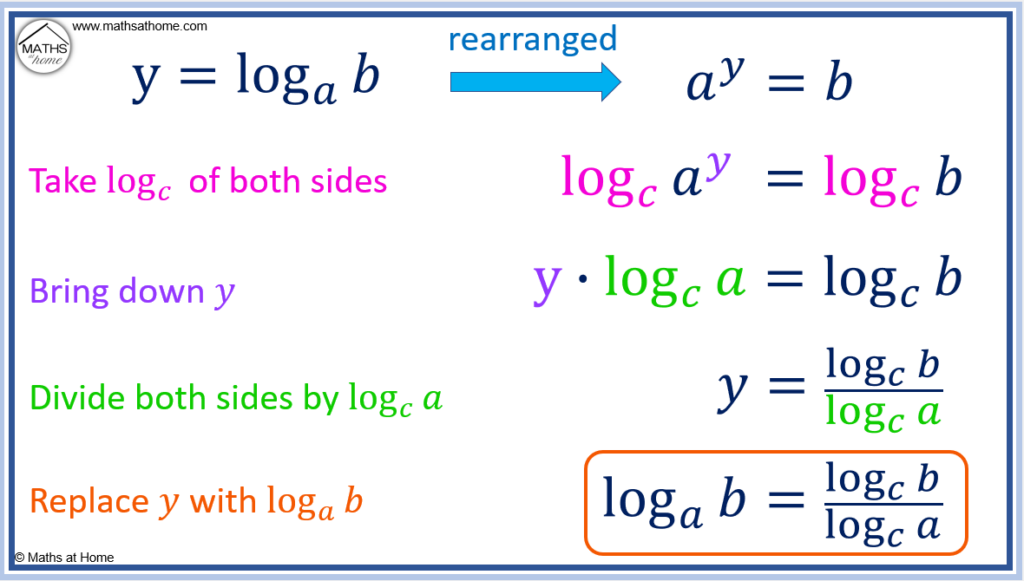



Related Post

Rich Zeoli Salary

1981 World Series MVP: A Look Back At The Champ Who Defined Piñera

Wayfair Financing: How Flexible Home Furnishing Loans Are Redefining Home Shopping

Jim Cantore: Standing at 6 Feet Tall, Unstoppable Force in Weather Reporting – Age, Height, and Career Impact

