The Mathematical Showdown: Odd Functions vs. Even Functions Explained

In the elegant framework of functional calculus, one pivotal distinction shapes how functions behave under symmetry: whether they are odd or even. These classifications determine fundamental properties about a function’s graph, integration behavior, and symmetry about the origin or the y-axis. Understanding this binary divide unlocks deeper insights into calculus, Fourier analysis, and even signal processing.

The contrast between odd and even functions is not merely theoretical—it directly influences computational methods, approximation strategies, and the interpretation of real-world phenomena.

Defining Odd and Even Functions: The Mathematical Core

At their core, odd and even functions are defined by symmetry with respect to the origin and y-axis, respectively. A function \textit{f}(x) is even if reemplazing\ x with–\ x yields the same output: \textit{f}(–x) = \textit{f}(x) for all x in the domain. Classic examples include cosine: \cos(–x) = cos(x), revealing symmetry about the y-axis, and the absolute value function |x|, which mirrors across the origin’s center.

In contrast, odd functions satisfy \textit{f}(–x) = –\textit{f}(x).

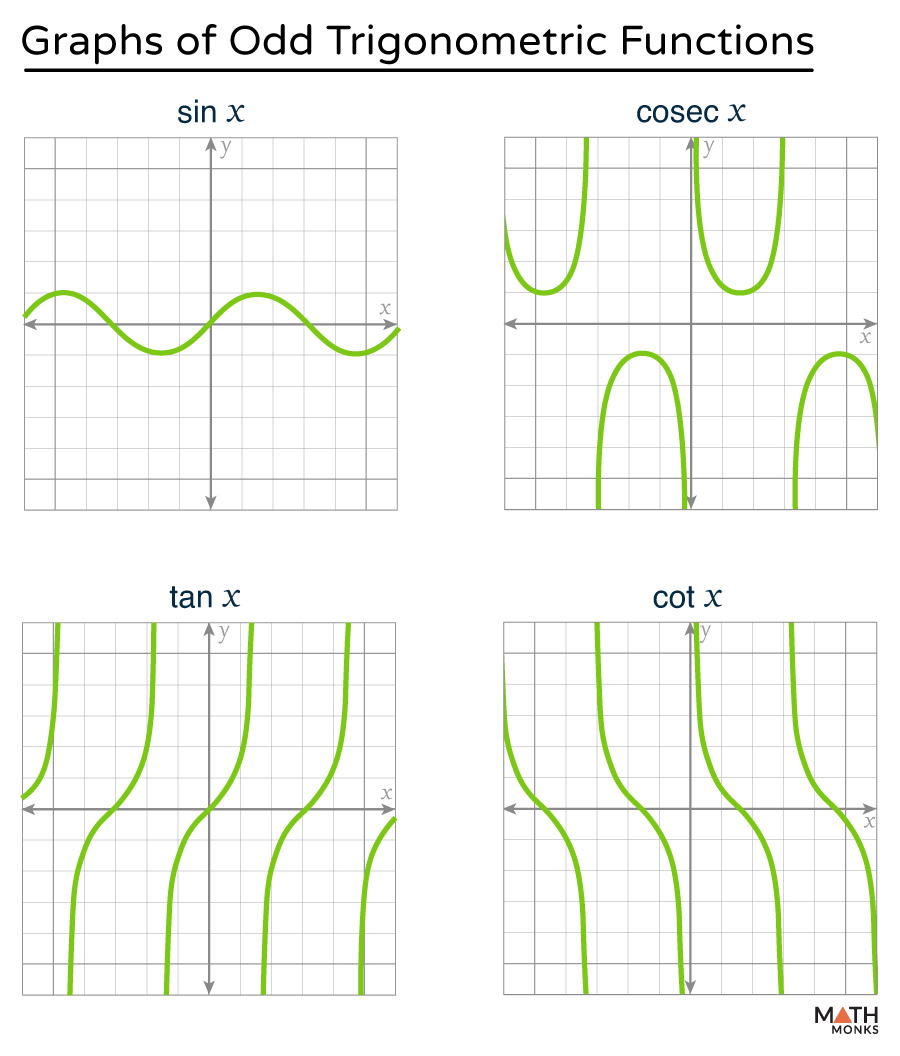
This rotational symmetry about the origin means the graph passes through (0,0) and exhibits flip behavior under 180-degree rotation. Functions such as sine – where sin(–x) = –sin(x) – or the identity x under all operations – perfectly illustrate this characteristic. These definitions form the backbone of function classification, governing how transformations and integrals unfold across mathematical domains.

Symmetry in Graphs: Visualizing the Divide

A function’s symmetry is immediately evident when analyzed through graphing.

Even functions produce plots symmetric about the vertical y-axis, allowing reflections across this line with no distortion. The butterfly-shaped curve of cos(x), for instance, remains unchanged when flipped over the y-axis.

Odd functions, by contrast, demonstrate rotational symmetry about the origin. When rotated 180 degrees around (0,0), the graph maps onto itself, flipping both vertically and horizontally.

Plotting y = sin(x) reveals this behavior: the negative portion of the curve aligns perfectly with the positive side, proving fundamental odd symmetry.

Mathematical Properties: Beyond Symmetry

Odd and even functions possess distinct algebraic and analytic properties with far-reaching consequences.

• Integrals over symmetric intervals: For an odd function, the definite integral over a symmetric interval [–a, a] is always zero.

  This arises because positive and negative halves cancel exactly. For even functions, the integral equals twice the area over [0, a], leveraging symmetry to simplify computations.

• Taylor series: Even functions admit only even-powered terms—think x², cos(x), or x⁴—while odd functions contain only odd powers—like x, sin(x), or x³. This term classification shapes convergence and approximation methods.
• Product and composition behavior: The product of two even functions remains even, and so does the product of two odd functions.

  However, odd × even yields odd, and even × odd produces odd. These rules guide functional manipulation in calculus and differential equations.

• Fourier series: In harmonic analysis, even and odd components of periodic functions are isolated by projection. Even functions contribute only cosine terms, odd ones only sine terms—enabling efficient signal decomposition.

These mathematical traits are not just abstract curiosities; they define how functions behave under transformation and integration, shaping analytical strategies across applied domains.

Real-World Impact: Applications Across Science and Engineering

The odd/even dichotomy extends well beyond pure mathematics.

In physics, parity—the symmetry under spatial inversion—classifies quantum states and crystallographic structures. Even functions describe even-parity phenomena (e.g., symmetric charge distributions), while odd functions govern odd-parity systems like electron transition moments.

In signal processing, decomposition into odd and even components allows engineers to filter noise, design band-limited systems, and optimize communication algorithms. Fourier analysis, foundational in audio processing and image compression, relies precisely on this skill.

An audio signal’s harmonic content is split into even (cosine) and odd (sine) spectral elements—for precise filtering and reproduction.

In electrical engineering, causal systems and time-invariant responses often exhibit even symmetry for stability, while transient odd responses signal switching behavior. Understanding these properties ensures accurate modeling and component design, improving reliability and performance in circuits and signal chains.

The Unseen Enigma: Why the Distinction Matters

What begins as a simple symmetry classification reveals profound depth. Odd and even functions act as mathematical archetypes—mirroring nature’s balance, from pendulum vibrations to electromagnetic waves.

Their behavior governs integration limits, wave decomposition, and symmetry-based physical laws. The divide between odd and even functions is not a trivial detail but a cornerstone of functional analysis.

Engineers, physicists, and mathematicians alike leverage this duality to simplify problems, uncover hidden patterns, and build sophisticated models.

It is a triumvirate of mathematical insight: symmetry in form, clarity in application, and precision in consequence.

By mastering odd versus even functions, one gains a lens through which to see order beneath complexity—where every f(x) reveals consistency, every graph aligns with logic, and every equation begins to speak in geometric terms. This binary classification, though elementary in nature, remains indispensable in both theoretical exploration and practical innovation.