The Power Behind Cos Sin Tan: Unlocking Complex Trigonometry for Engineering and Science

In the intricate dance of wave mechanics, signal processing, and structural design, the trigonometric identity Cos Sin Tan emerges as a sharp, precise tool—bridging the gap between theoretical elegance and real-world application. Though often overlooked in casual discussion, Cos Sin Tan—defined as cos(θ)·sin(θ)—plays a critical role in fields ranging from electrical engineering to robotics, enabling engineers and scientists to model oscillatory behavior, simplify signal analysis, and optimize mechanical systems with elegance. Far more than a mathematical curiosity, this function underpins phenomena that shape modern technology, from alternating current systems to advanced sensor calibration.

There is a reason Cos Sin Tan stands out in technical curricula: it elegantly captures the interplay between cosine and sine in scaling periodic motions, particularly where phase relationships matter. “Understanding Cos Sin Tan is like holding a universal lever—applied where angles dictate wave shape, amplitude efficiency, or system response,” notes Dr. Elena Marquez, a senior engineer specializing in power electronics.

“It’s not just about solving equations; it’s about predicting behavior.”

At its core, Cos Sin Tan is the product of two fundamental trigonometric functions: cosine, which measures horizontal projection, and sine, which captures vertical displacement. Written mathematically as: Cos(θ) · sin(θ) = ½ sin(2θ), this identity arises directly from the double-angle formulas, revealing a compact yet powerful form that simplifies complex calculations. The dual nature of the expression reflects a deeper symmetry—cosine’s stabilizing influence multiplied by sine’s dynamic shift—making it indispensable in systems involving periodic variation.

This identity is not merely elegant notation; it is computationally transformative. When modeling signals in the frequency domain, sinusoidal transformations often involve products of sinusoids. Cos Sin Tan emerges naturally in integrals and derivatives involving these products, where it enables substitution techniques that reduce otherwise intractable expressions into solvable forms.

One of the most significant practical applications of Cos Sin Tan lies in electrical engineering, particularly in the analysis of alternating current (AC) circuits. In AC systems, voltage and current vary sinusoidally with time, often differing in phase due to reactive components like inductors and capacitors. Engineers rely on Cos Sin Tan to compute power dissipation, especially reactive power, which depends on the phase difference between voltage (cosine-driven) and current (possibly sine-shifted).

The real power consumed in such circuits is proportional to the average value of cos(ϕ), where ϕ is the phase angle—scenarios directly accessible through the Cos Sin Tan framework. As industry professional Raj Patel explains, “When designing efficient inverters or power supplies, we use Cos Sin Tan to predict how much energy actually translates into heat or mechanical work—not just raw voltage and current, but their angular relationship.” This predictive power reduces energy waste and improves system lifespan.

Beyond electricity, Cos Sin Tan finds critical utility in mechanical and control systems.

In robotics, for example, joint actuators generate oscillatory motion requiring precise timing and force control. The position and torque profiles of robotic limbs are often modeled using sinusoidal functions, and Cos Sin Tan enables accurate simulation of these dynamics, especially in feedback loops that demand phase-sensitive corrections. Similarly, in structural engineering, seismic response analysis uses harmonic excitation models where displacement, velocity (sinusoidal), and acceleration (derivative of sine) all interact.

Cos Sin Tan helps quantify resonance frequencies and damping ratios—key to designing buildings that withstand earthquakes. In digital signal processing, the identity supports efficient filtering and modulation schemes. Fast Fourier Transforms (FFT), central to audio compression and wireless communication, depend on decomposing signals into sinusoidal components.

When filtering or demodulating signals—such as separating voice from background noise in a call—operators exploit Cos Sin Tan to isolate frequency bands with minimal distortion, ensuring clarity and bandwidth efficiency.

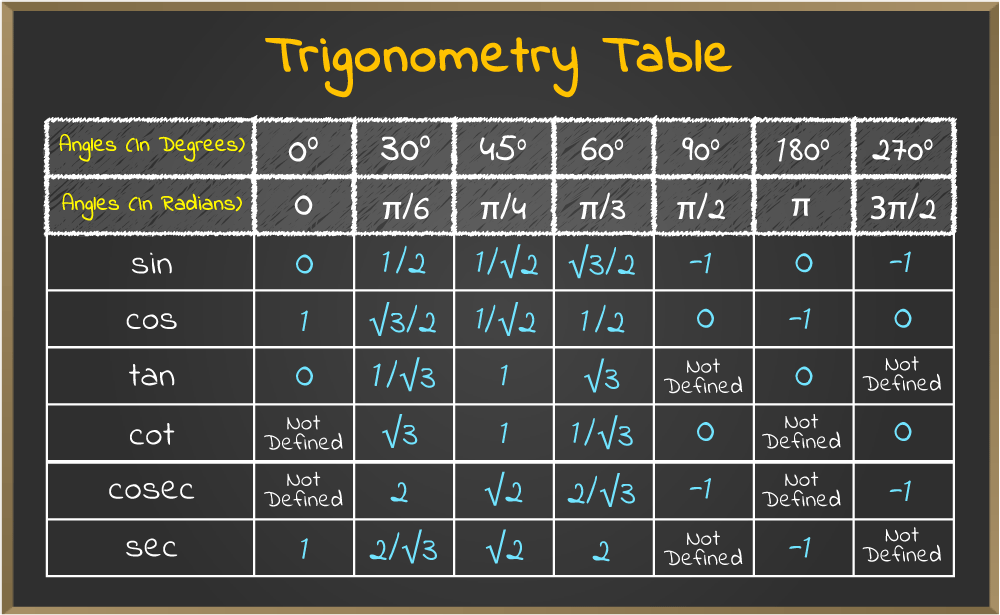
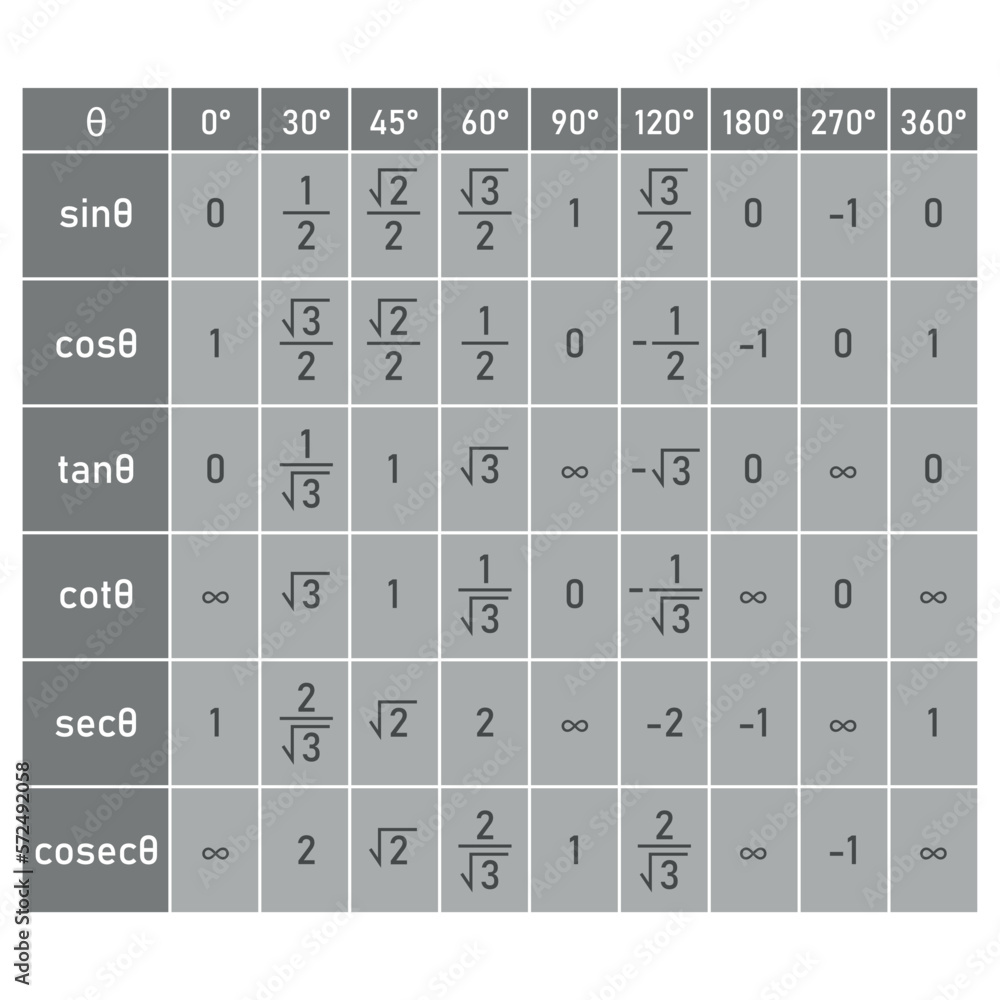
Mathematically, Cos Sin Tan operates across a defined domain where θ is an angle in radians, typically influencing functions in periodic intervals like [0, 2π). Its range spans from 0 to ½, peaking at θ = π/4 (where cos(π/4)·sin(π/4) = ½) and vanishing at θ multiples of π/2.

This bounded, smooth profile makes it ideal for modeling gradual transitions in systems where sharp discontinuities are unrealistic—common in physical phenomena involving vibration, wave propagation, or cyclical motion. Yet its utility extends beyond periodic functions. In calculus, the derivative of sin²(θ) yields 2 sin(θ) cos(θ), precisely Cos Sin Tan.

This makes the expression central to solving optimization problems involving area under curves, maxima, and minima of oscillating systems—such as determining peak efficiency in energy conversion devices or optimal timing in mechanical oscillators.

The teaching of Cos Sin Tan often poses a challenge, as students must reconcile its appearance in abstract formulas with tangible physical meaning. “It’s not just about memorizing identities,” emphasizes Dr.

Marquez. “It’s about seeing how a compact equation governs real behavior—like how motors smooth rotational motion or how microphones filter ambient sound.” Clarifying this connection transforms the learning process from mechanical repetition to insight. Hands-on tools—graphing calculators, interactive software, and lab experiments—help visualize how angle adjustments alter the amplitude of oscillation, reinforcing conceptual understanding.

Educators increasingly emphasize interdisciplinary applications to ground the concept. Magnaught interactive demonstrations show how tuning a speaker’s phase (via Cos Sin Tan relationships) eliminates distortion, proving the identity’s relevance beyond textbooks. This contextual learning fosters deeper retention and technical fluency.

As technology advances, the role of trigonometric identities like Cos Sin Tan grows more strategic. In artificial intelligence and machine learning systems modeling cyclical patterns—such as seasonal energy demand or wear cycles in machinery—these identities underpin predictive algorithms. Optimization routines leverage them to peer into periodic landscapes, identifying peaks and troughs with minimal computational overhead.

The efficiency they deliver is subtle but profound, fueling smarter systems across smart grids, autonomous vehicles, and industrial automation. With exascale computing handling ever-larger datasets, Cos Sin Tan remains a cornerstone—unseen yet indispensable. Its power resides not in flashy complexity but in quiet precision, quietly guiding engineers and scientists toward elegant, efficient solutions.

Cos Sin Tan is far more than a scholarly trifecta of cosine, sine, and tangent—it is a foundational force in modern science and engineering. Whether stabilizing power grids