Unlock Angular Precision: How a Trigonometry Calculator Transforms Complex Angle Solving

At the heart of navigation, construction, physics, and engineering lies an unseen mathematical force—trigonometry—where calculating unknown angles can mean the difference between success and failure. A Trigonometry Calculator serves as a precision tool in this domain, enabling instant solutions to problems involving triangles, periodic motion, and spatial relationships. Whether determining roof pitches, aligning satellite dishes, or modeling planetary orbits, this digital instrument simplifies what once required hours of manual computation and advanced trigonometric tables.

As both a learning aid and a practical device, the Trigonometry Calculator empowers users—from students to professionals—to uncover angles with accuracy, confidence, and speed.

From Right Triangles to Circular Rhythms: The Full Scope of Trigonometric Calculations

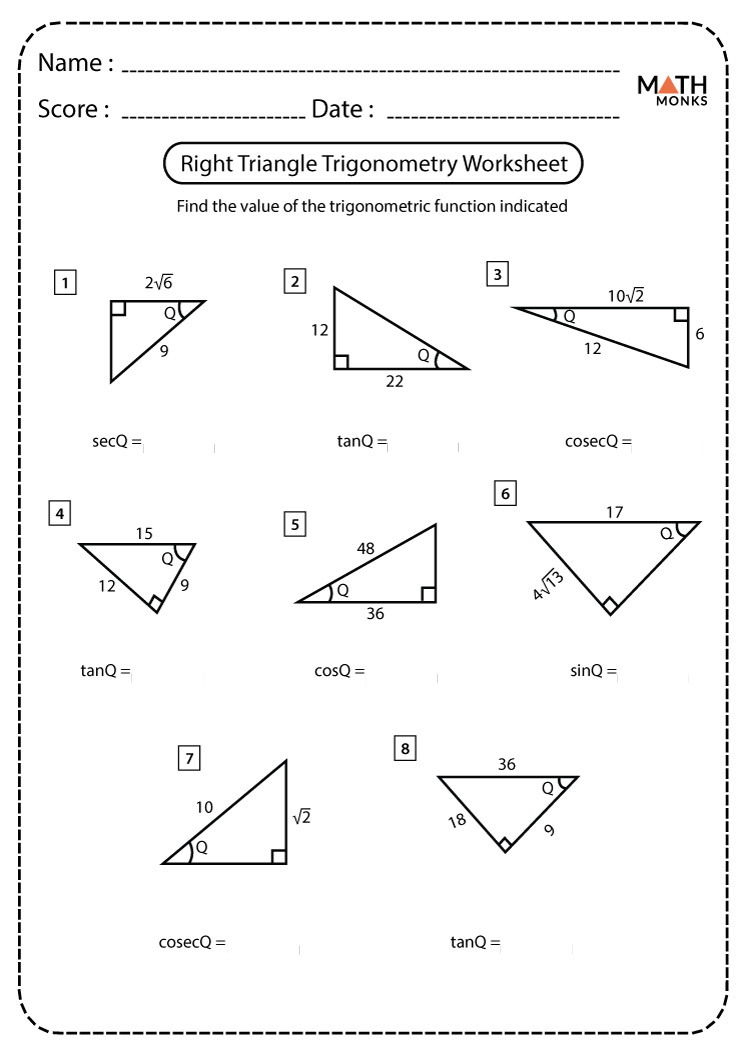
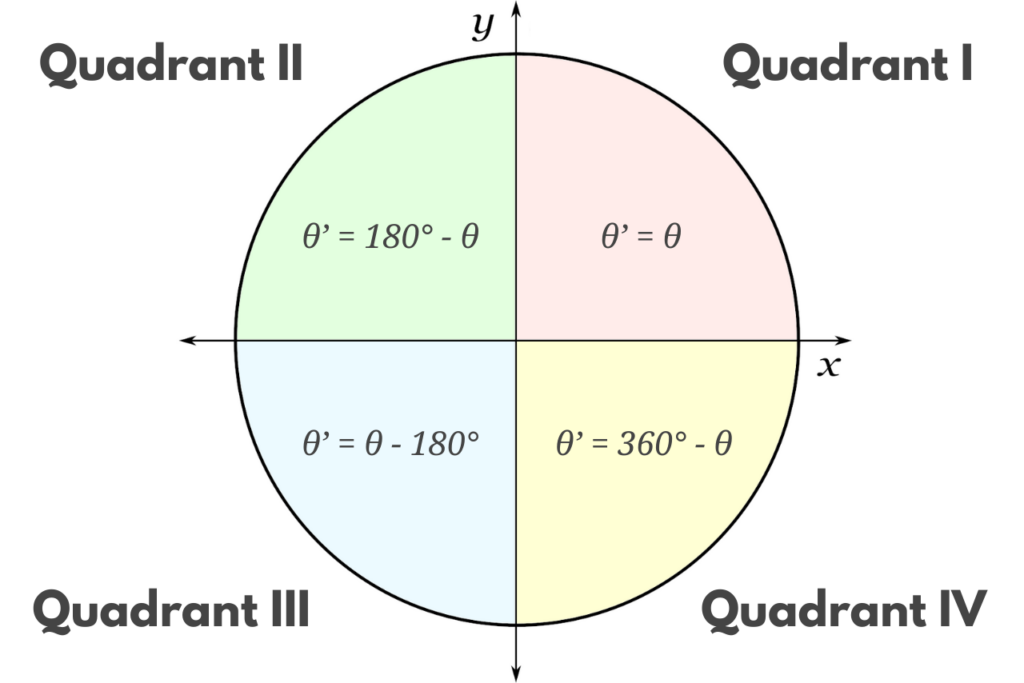
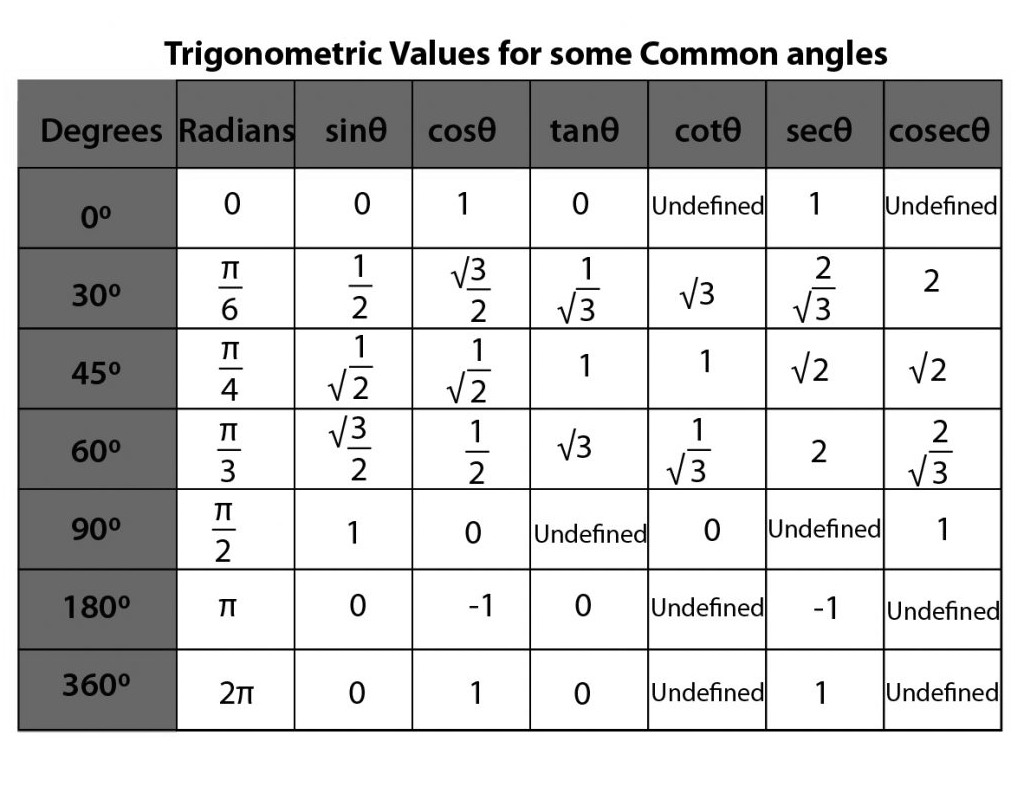
Trigonometry extends far beyond basic sine, cosine, and tangent ratios taught in early calculus. Its applications span right triangle analysis, unit circle navigation, wave mechanics, and vector decompositions.

A Trigonometry Calculator integrates these domains, handling calculations involving acute, obtuse, and even abstract angles across multiple quadrants and domains. Key functions include solving for unknown angles when two sides or angles are known—via the Law of Sines and Cosines—determining side lengths using the Pythagorean Theorem, and evaluating angular relationships in non-right triangles. Law of Sines proves indispensable when two angles and one side are known, or two sides and the non-included angle.

The formula, \text{sin}\ A : \sin \beta : \sin \gamma = a : b : c allows users to plug in measurements directly, instantly revealing missing angles. Meanwhile, Law of Cosines extends solution to any triangle when two sides and the included angle—or all three sides—are provided: \text{c}^2 = a^2 + b^2 - 2ab\cos\gamma.

These automated processes eliminate the trial-and-error of slide rules and hand-featured tables, ensuring results consistent with theoretical principles.

For instance, a surveyor measuring a riverside cliff can input distances and angles, using the calculator to determine a navigation reference point—no formula rewriting required.

Wave Behavior, Orbital Mechanics, and Beyond: Real-World Applications Powered by Precision Angles

In physics, angular calculations underlie the behavior of oscillating systems. The periodic motion of pendulums, alternating currents, and even musical harmonics depends on phase angles that a Trigonometry Calculator computes with reliability.

Similarly, engineers inspecting satellite trajectories rely on precise angular inputs to align antennas or adjust orbital inkjet maneuvers, where millimeter-level errors compound across vast distances. Construction professionals use trigonometric tools to verify roof slopes—critical for water runoff and structural stability—by measuring rise and run with surveying lasers linked to real-time calculators. A roof with a 5:12 pitch implies a 22.6° angle, a value easily calculated using inverse tangent (arctan) functions embedded in most calculators: \text{angle} = \tan^{-1}(rise/run).

This direct application transforms architectural blueprints into built reality. Moreover, in astronomical observation, calculating the angle of celestial bodies from Earth involves adjusting for latitude and time zones—processes simplified by calculators that factor in spherical trigonometry and time-based coordinate shifts.

Functionality Built for Ease: How a Trigonometry Calculator Simplifies Different Angle Types

Modern Trigonometry Calculators are designed with user experience in mind, offering interfaces that handle multiple problem types seamlessly.

Users input known values—whether a side length, angle, or a combination—and receive immediate output in degrees or radians, often with supporting explanations of used laws or formulas. Some advanced models include graphical plots, letting users visualize triangle shapes, phase shifts, or waveforms alongside computed solutions. Administrative features such as query history, unit conversion, and step-by-step breakdowns enhance learning and auditability.

Students verifying homework errors find clarity, while architects cross-check structural angles without reference back to textbook solutions. This combination of speed and transparency accelerates user fluency. Real-World Example: A robotics technician programming joint rotations must determine minimum servo angles for precise arm positioning.

Using inverse trigonometric functions, the calculator computes exact servo inputs based on target coordinates in Cartesian space, translating spatial demands into motion with millidegree precision.

The Future of Angle Calculation: Accuracy, Accessibility, and Automation

As educational tools and engineering software evolve, the Trigonometry Calculator remains a foundational instrument—bridging theory and practice through instant, accurate computation. Its role grows more vital in an age where automation and simulation dominate design and diagnostics.

Whether used in a classroom, drone operation lab, or manufacturing floor, this tool ensures angles are no longer enigmas, but calculable pathways to innovation. The precision facilitated by a Trigonometry Calculator extends far beyond textbooks. It enables smarter navigation, stronger infrastructure, reliable energy systems, and groundbreaking scientific discovery.

In every