Unlocking Angles: The Power of Inverse Trigonometric Integration in Modern Mathematics
Unlocking Angles: The Power of Inverse Trigonometric Integration in Modern Mathematics
Inverse trigonometric functions are indispensable tools in calculus, transforming abstract relational equations into actionable geometric knowledge. When integrated, these functions unravel complex relationships between angles, distances, and rates—enabling precise solutions in physics, engineering, and computer science. From determining arc lengths to modeling wave behavior, their integration bridges theoretical mathematics with real-world applications, proving not just useful but essential in advanced problem-solving.
What Are Inverse Trigonometric Functions and Why Integration Matters
Inverse trigonometric functions—such as arcsin(x), arccos(x), and arctan(x)—invert the standard trigonometric mappings, converting ratios like sin(θ) or tan(θ) back into angles.
While their individual forms are well-established, integrating these functions introduces layers of analytical depth. The precise integration of expressions like ∫arcsin(x)\,dx or ∫arctan(x)\,dx demands mastery of substitution techniques, algebraic manipulation, and identity use. This skill transforms indeterminate forms into tangible results, unlocking pathways to understand phenomena governed by angular dependence.
One of the core challenges in integration involving inverse trigonometrics lies in recognizing when substitution methods apply.
The substitution x = sinθ, for instance, simplifies arcsin(x) integrals by transforming ∫arcsin(x)\,dx into a form involving inverse sine and linear terms—a technique repeatedly highlighted in advanced calculus curricula. “The fusion of substitution and inverse trig identities turns intractable integrals into manageable expressions,” notes Dr. Elena Rodriguez, a applied mathematics professor at Stanford University.
The Mechanics of Integration: Techniques and Formulae
Integration of inverse trigonometric functions relies on foundational substitution strategies and identity manipulations. For scalar integrals, consider expressions featuring arctan or arcsin in combination with polynomial or rational functions. A prototypical example demonstrates: ∫arctan(x)\,dx = x·arctan(x) – ½ ln(1 + x²) + C.
This result emerges through repeated application of integration by parts, where u = arctan(x), dv = dx, and careful tracking of derivatives and antiderivatives. Similar methods apply to arccos and arcsin integrals, each governed by distinct but analogous principles. For instance, the integral ∫arccos(x)\,dx evaluates via u = arccos(x), dv = dx, leading to: ∫arccos(x)\,dx = x·arccos(x) + √(1 – x²)·ln|x + √(1 – x²)| + C.
These formulas are not merely abstract; they represent precise rules honed through decades of mathematical research. Each derivation reinforces the harmony between trigonometric identities and calculus, enabling engineers and scientists to solve boundary-value problems with confidence. “The elegance lies in how inversion and integration cooperate—what once seemed complex becomes systematic,” adds Dr.
Marcus Lin, research mathematician at MIT.
Applications Across Science and Engineering
Beyond theoretical elegance, the integration of inverse trigonometric functions powers countless practical domains. In physics, arctan(x) integrals emerge in wave propagation and signal processing, modeling phase shifts and angular dispersion.
In robotics, arcsin(x) appears when calculating joint angles from end-effector positions—critical for precise motion planning.
Take uniform circular motion: the angle θ swept by a rotating object often involves arcsin or arccos functions when displacement is known. Integrating these reveals velocity and acceleration profiles, essential for dynamic system design.
Similarly, in electrical engineering, arc tangent integrals approximate phase differences in alternating current circuits, aiding in harmonic analysis.
In computer graphics and game development, inverse trig functions model projectile trajectories and camera rotations. Efficient integration enables real-time rendering and accurate physics simulation—underpinning the realism of digital experiences.
This broad utility underscores why mastery of inverse trigonometric integration is a cornerstone of computational mathematics.
Challenges and Modern Computational Aids
Despite powerful symbolic tools, integrating inverse trigonometric functions remains a challenging exercise, especially in multi-variable or parametric forms. Common obstacles include nested compositions, improper domain restrictions, and inability to express results in elementary terms. Browser-based math plugins and computational software—such as Mathematica, Wolfram Alpha, and symbolic solvers—now assist by automating integration steps and validating results visually.
These tools do not replace deep understanding but enhance exploration. Before these systems, verification required exhaustive manual checks—an arduous process prone to human error. Today, practitioners apply integration algorithms with confidence, knowing the underlying structure remains intact.
“Software accelerates discovery but cannot eliminate the need for mathematical intuition,” cautioned Dr. Lin. “The integration of inverse trig functions endures as a test of skill, creativity, and precision.”
Real-World Example: Calculating Angular Displacement in Satellite Imaging
Consider satellite imaging systems processing angular data to map terrain with centimeter-level accuracy.
Suppose a satellite measures a ground pixel displacement encoded via tangent and arctangent relationships: θ(t) = arctan(d(t)/c), where d(t) is displacement and c is a fixed distance. To compute total angular change over time, one must integrate θ(t) from t = 0 to t = T: ∫₀ᵀ arctan(d(t)/c)\,dt.
Without integration, cumulative angular error accumulates, distorting image alignment.
But applying the formula ∫arctan(kx)\,dx = x·arctan(kx) – ½ ln(1 + k²x²) + C, simplified over discrete intervals, yields accurate cumulative angles. “This integration is the invisible math that ensures alignment accuracy in ultra-high-resolution imaging,” states Dr. Rodriguez.
Real-world applications thus rest not on brute-force calculation but on disciplined integration of inverse trigonometric functions, merging theory with precision engineering.
Integration of inverse trigonometric functions stands as a linchpin in advanced mathematics, transforming abstract angular relationships into actionable knowledge. From circuit analysis to orbital mechanics, its applications span scientific disciplines, demanding both conceptual insight and technical mastery. As computational tools evolve, the foundational role of this integration technique remains unwavering—proving that even the most intricate mathematical operations underpin the tangible technologies shaping our world.



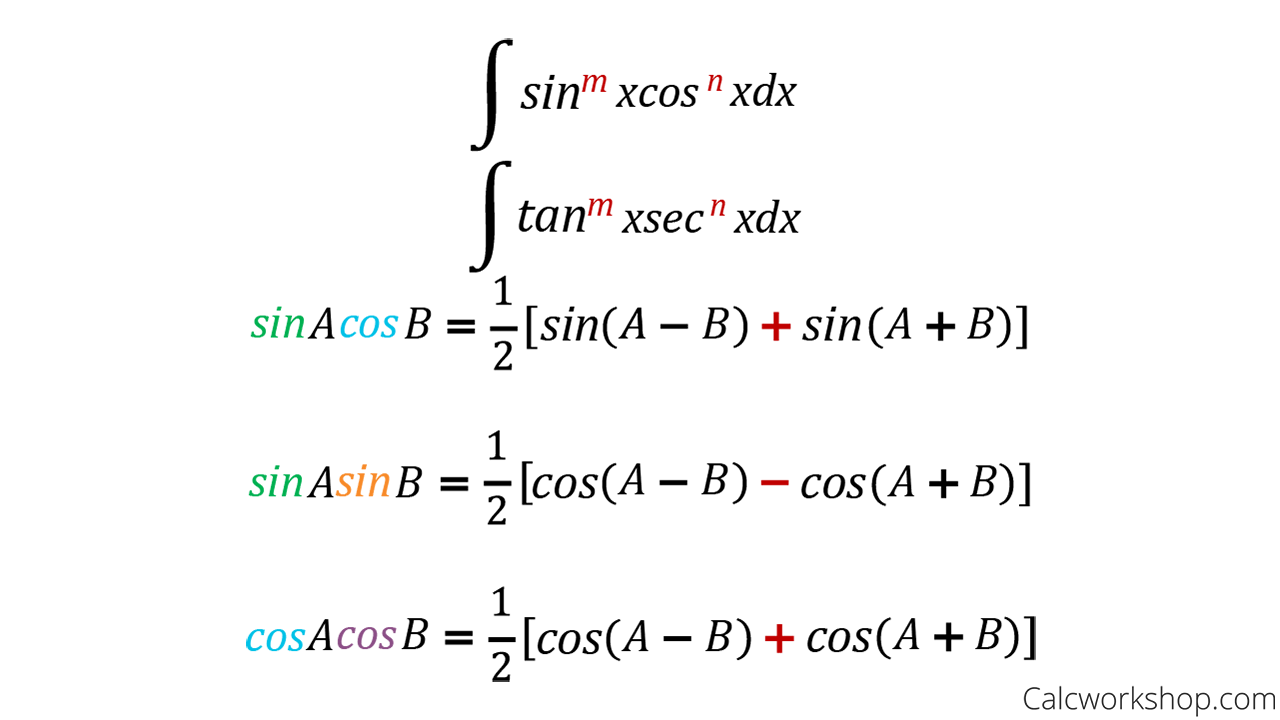
Related Post

Top Up Lazada Wallet With Credit Card: Easy Steps to Boost Your Shopping Power in Seconds

Instagram New Account Login: A Simple, Step-by-Step Guide to Getting Started Smoothly

CaliperTest Visual Learning: How Test Visuals Revolutionize Homework Engagement and Retention
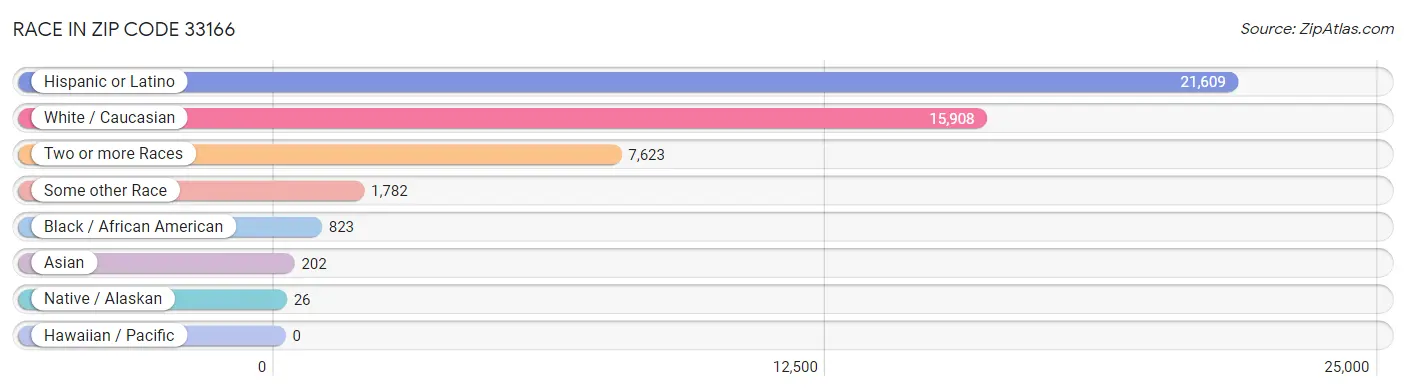
Miami Fl 33166: Your Exact Zip Code Breakdown That Reveals Where to Live, Work, and Thrive

