Unlocking Data Precision: How Variance Formula Transforms Uncertainty in Statistical Analysis
Unlocking Data Precision: How Variance Formula Transforms Uncertainty in Statistical Analysis
Statistical analysis hinges on understanding variability — the measure of how spread out data points are from their average. The variance formula stands as a cornerstone in quantifying this spread, enabling researchers, analysts, and scientists to draw meaningful insights from noise. From finance to epidemiology, variance provides a rigorous foundation for assessing risk, consistency, and reliability.
But beyond its theoretical weight, the practical application of variance — through the variance formula — reveals deeper patterns hidden within datasets, informing decisions with statistical confidence. This article delves into the mechanics, evolution, and real-world impact of the variance formula, exploring how it transforms raw data variance into actionable knowledge. What Is the Variance Formula — and Why It Matters At its core, the variance formula quantifies the average squared deviation of data points from the mean, capturing the degree of dispersion within a dataset.
Mathematically defined as \\[ \\text{Var}(X) = \\frac{1}{N} \sum_{i=1}^{N} (X_i - \\mu)^2 \\], where \\(X_i\\) denotes individual data values and \\(\\mu\\) is the population mean, this formula provides a standardized measure of variability. Unlike simpler metrics such as range or interquartile range, variance incorporates every data point through squaring deviations, intensifying the impact of outliers and ensuring no signal of spread is minimized. The formula’s elegance lies in its balance of mathematical rigor and intuitive clarity.
By squaring differences, variance avoids canceling positive and negative deviations — a critical feature that preserves directional information. For instance, in a financial portfolio with fluctuating returns, variance reveals not just average performance but also volatility, a key indicator of risk. As statistician George E.
P. Box once noted, “All models are wrong, but some are useful” — the variance formula exemplifies this wisdom, useful across contexts despite inherent simplifications.
The formula’s utility extends beyond descriptive statistics.
In inferential analysis, variance forms the basis for standard error, confidence intervals, and hypothesis testing. Without it, statistical inference would lack precision, turning meaningful data into guesswork. Its role as a foundational tool underscores why mastery of variance is indispensable for data scientists, economists, and engineers alike.
Breaking Down the Components: How Variance Is Calculated and Interpreted Understanding variance demands clarity on its formula’s structure and interpretation.
The standard single-sample variance emphasizes three core elements: data size, mean reference, and deviation squaring.
The formula splits naturally:
1. **Data collection**: A finite dataset, whether finite (N known) or infinite (with a known theoretical distribution), provides individual values.2. **Mean computation**: The arithmetic mean (\\(\\mu\\)) anchors the analysis, representing central tendency. 3.
**Deviation adjustment**: For each value, the formula calculates \\((X_i - \\mu)^2\\), squaring the deviation to eliminate sign bias and amplify larger outliers. This squaring step makes variance sensitive to extreme values — a strength for risk analysis but a point of caution when data includes errors. The resulting value is expressed in squared units of the original data, which can challenge interpretation.
For example, variance of test scores in centimeters squared feels abstract until converted to standard deviation — the square root of variance — restoring intuitive units like meters or inches.
Graphical tools deepen comprehension. Variance appears prominently in the animated ellipses of statistical tutorials — shrinking with higher variance, expanding with dispersion.
These visual cues ground abstract numbers into spatial intuition, revealing how data spreads tightly around the mean or flares outward. Real-World Applications: From Finance to Forensics Wherever quantitative uncertainty matters, variance plays a pivotal role. In finance, portfolio managers rely on variance to measure asset volatility.
A stock trading between $50 and $150 shows higher variance than one stable at $60, guiding risk-return tradeoffs. The Sharpe ratio, a performance metric, explicitly uses variance in its denominator, penalizing high volatility despite high returns. In clinical trials and epidemiology, variance informs study reliability.
High variance in patient response to a drug suggests inconsistent effects, prompting further investigation. Conversely, low variance across trial sites strengthens confidence in treatment efficacy — a crucial insight for regulators and pharmaceutical firms. Climate scientists deploy variance to analyze weather patterns.
Long-term temperature datasets reveal variance shifts, signaling climate instability. A rising variance in annual averages over decades underscores not just warming, but increasing volatility — heatwaves and cold snaps becoming more frequent and severe. Variance vs.
Standard Deviation: Two Sides of the Same Coin While variance quantifies squared spread, its square root yields standard deviation — a more interpretable metric in many applications. Standard deviation, measured in original units, translates variance’s abstract numbers into tangible insights. For instance, a standard deviation of 2°C in global temperatures offers direct relief to policymakers, whereas variance of 4°C² lacks immediate intuitive force.
Yet, variance remains indispensable in statistical theory. It is the building block of key inferential tools — analysis of variance (ANOVA), regression diagnostics, and Monte Carlo simulations — where squared terms underpin risk modeling and confidence interval construction. The formula’s dual role — abstract in isolation, practical in integration — defines its enduring relevance.
The Variance Formula in the Digital Age: Tools and Challenges Advancements in computing have revolutionized variance computation. Spreadsheets automate summation and averaging; programming languages like Python and R offer built-in variance functions with \\(np.std\\) and \\(np.var\\), minimizing manual error. Yet, computational power demands vigilance: outliers, missing data, and sampling bias can distort results.
Multiple sampling techniques and robust variance estimators — such as Huber-White standard errors — now address data complexities once limiting traditional formulas. These innovations extend variance’s utility into big data and machine learning, where model stability and prediction uncertainty must be quantified with precision. Mastering Variance: A Skill for Data-Driven Futures 操戍 over clarity, the variance formula is not merely a formula — it is a lens through which variability becomes measurable, predictable, and manageable.
Its power lies in translating uncertainty into quantifiable risk, instability into actionable insights. Whether assessing investment portfolios, validating clinical studies, or modeling climate change, variance offers a rigorous foundation for informed decision-making. As data permeates every sector, fluency in statistical principles — anchored by the variance formula — emerges as essential.
Understanding how variance captures the silk and stiffness of data spread empowers analysts to turn chaos into clarity, risk into insight, and numbers into decisions that shape our world.
From classroom statistics to boardroom forecasts, the variance formula remains a silent architect of statistical certainty — reliable, precise, and indispensable. It turns a collection of numbers into a story of stability and change.



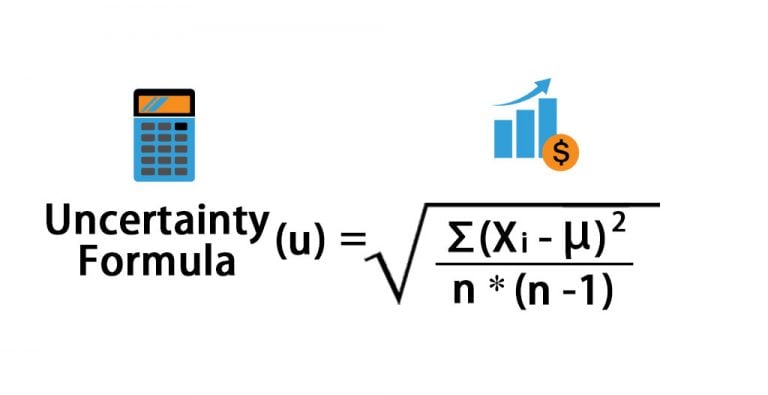
Related Post

Unlock Hidden Relationships: How Covariance Formula Transforms Data Insights

How TVN’s Live Wire Illuminates the Pulse of South Korea’s Dynamic Entertainment Industry

Who Is Chan Charlie? All About the Rising Star Capturing Global Attention
Where the Wild Things Are: The Enduring Magic of Louis Sedlacek’s Beloved Illustration

