Unlocking Precalculus: How Limits and Graphing Illuminate Complex Behavior

In the intricate world of precalculus, understanding function behavior near undefined points or asymptotes remains a pivotal challenge—yet limits and graphing techniques, when integrated through structured approaches like PDF-based visual frameworks, transform abstract concepts into intuitive insights. By combining analytical rigor with dynamic graphical representations, learners gain a powerful toolkit to interpret continuity, discontinuities, and long-term trends with precision. The Precalculus With Limits Graphing Approach PDF emerges not merely as a study aid but as a foundational method for uncovering the hidden logic behind complex functions.

The Power of Limits: Bridging Algebra and Geometry

Limits serve as the cornerstone of calculus, capturing the behavior of functions as input values approach specific points—whether finite, infinite, or irrational.

In precalculus, mastering limits enables students to diagnose discontinuities, define asymptotic behavior, and analyze convergence, all essential for graphing accuracy. Unlike rote memorization, a limits-focused approach emphasizes the “why” behind asymptotic trends. As noted by mathematician Francis Su, “Limits are the bridge between discrete calculations and continuous motion—their mastery allows students to ‘see’ the shape of functions before they are drawn.”

Key limit concepts—such as one-sided limits, infinite limits, and limit laws—form the analytical backbone for interpreting function behavior.

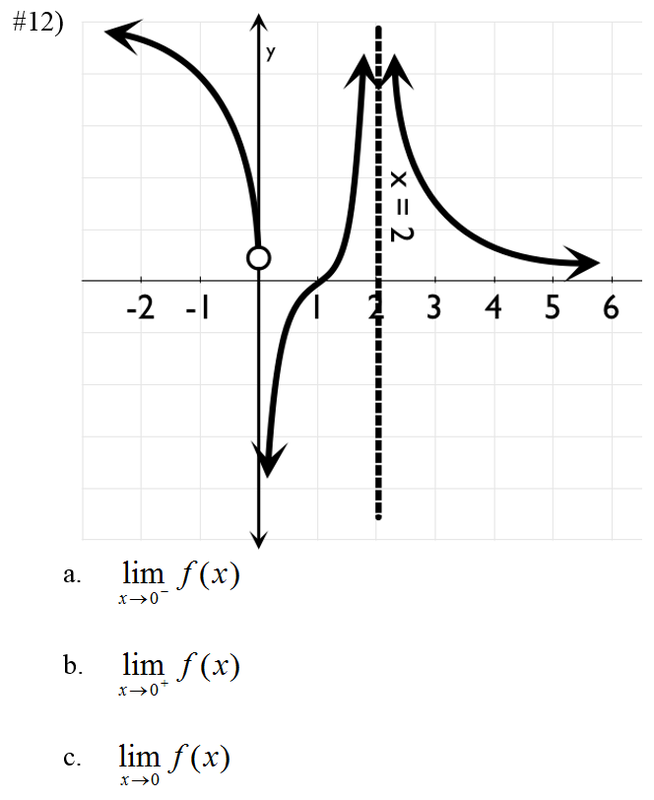
For instance, the limit \[ \lim_{x \to 2^-} \frac{1}{x - 2} = -\infty \] clearly signals a vertical asymptote at \( x = 2 \), a signal directly transferable to graphing. These analytical clues empower students to anticipate graph features without merely plotting points.

Graphing with Limits: Translating Behavior into Visual Clarity

Graphing is not just a visual check—it is a language through which limits are made tangible. The Precalculus With Limits Graphing Approach PDF integrates limit-based insights directly into graph construction, turning analytical results into intuitive representations.

Students learn to annotate graphs with asymptotes, holes, and unbounded growth by referencing calculated or approximated limits at critical points. For example, consider the rational function \[ f(x) = \frac{x^2 - 1}{x - 1} \] which simplifies to \( x + 1 \) for \( x \ne 1 \). Though undefined at \( x = 1 \), the limit \[ \lim_{x \to 1} f(x) = 2 \] reveals a removable discontinuity—a point where the graph “hugs” the line \( y = x + 1 \) but strikes a hole.

The PDF illustrates this by showing the undefined point marked with a hole, while the graph smoothly approaches \( y = 2 \) on either side, merging algebra and visualization.

Advanced functions, including piecewise, exponential, and trigonometric types, benefit equally from this synergy. Consider the function \[ f(x) = \frac{\sin x}{x} \] for \( x \ne 0 \); although undefined at zero, its limit \[ \lim_{x \to 0} \frac{\sin x}{x} = 1 \] is a canonical example of a removable discontinuity, often visualized via asymptote-like behavior near zero in graphing tools. By embedding such limit logic in PDF-based graphing guides, students master not just “where” features appear but “why” and “how”—deepening conceptual retention.

Practical Applications: From Theoretical Concepts to Real-World Modeling

The integration of limits and graphing via PDF-driven frameworks extends beyond exams—it supports real-world modeling.

Engineers, economists, and data scientists rely on precalculus concepts to simulate phenomena like population growth, decay processes, or supply-demand curves. In each case, limits uncover long-term limits, stability points, and inflection behavior. For instance, a logistic growth model \[ P(t) = \frac{L}{1 + e^{-k(t - t_0)}} \] exhibits asymptotic behavior as \( t \to \infty \), approached but never exceeding \( L \)—a limit-driven insight visually confirmed through carefully annotated graphs.

PDF learning modules often include annotated case studies, demonstrating how analytical limits directly inform accurate, predictive graphs.

Moreover, technology integration enhances this approach: interactive PDFs allow students to manipulate function parameters and instantly observe how changes induce shifts in limits and graph形貌. This dynamic interplay reinforces cause-and-effect relationships—transforming passive learning into active discovery.

The Evolution of Precalculus Instruction: Why Visual Limits Matter

The traditional divide between algebra and calculus blurs when limits and graphing are taught in tandem through structured PDF resources. Cognitive research confirms that dual-coding—visual and symbolic representation—significantly boosts comprehension and recall.

The Precalculus With Limits Graphing Approach PDF capitalizes on this, presenting learners with: - Step-by-step limit evaluations structured for clarity; - High-fidelity graphs annotated with precise limit-based notes; - Practical examples ranging from elementary rational functions to advanced piecewise models; - Exercise sets where students predict behavior before graphing, then verify outcomes. Such scaffolding fosters not just procedural fluency but conceptual mastery. As educational theorist Dr.

G. E. Young observes, “Teaching limits through graphs turns abstract numbers into spatial stories—students learn to ‘read’ mathematics spatially and numerically.”

Mastering Precalculus Through Limits and Graphs: A Path to Deep Understanding

The synergy of limits and graphing, as presented through resource-rich PDF approaches like Precalculus With Limits Graphing Approach PDF, redefines how students engage with precalculus.

By anchoring abstract analytical ideas in visual, intuitive contexts, learners transform from passive calculators into active mathematicians. This method does more than improve test scores—it cultivates a robust, enduring understanding of function behavior, essential not only for future calculus success but for data-driven reasoning across disciplines. In an era where quantitative literacy defines problem-solving fluency, this integrated approach stands as a cornerstone of effective precalculus education—where limits illuminate, graphs reveal, and knowledge becomes visible.