Unlocking Quadratic Secrets: How the Math of Curves Powers Quadratic Formula Physics
Unlocking Quadratic Secrets: How the Math of Curves Powers Quadratic Formula Physics
When solving motion under constant acceleration, physics relies almost exclusively on quadratic equations—equations defined by the powerful quadratic formula. From projectile paths to electric circuits, the mathematics behind how objects move through space is rooted in the simple yet profound structure of quadratics: ax² + bx + c = 0. Understanding how this formula emerges from standard kinematic equations reveals a deeper connection between algebra and the physical world, transforming abstract equations into tools that predict real motion.
With the quadratic formula as a bridge between theory and observation, physicists and students alike gain a precise method to decode the dynamics of free fall, parabolic trajectories, and resonance phenomena.
From Kinematics to Quadratics: The Physics Behind the Formula
Every free-fall motion or projectile launch follows a predictable trajectory governed by classical mechanics. Consider an object dropped or launched vertically: its displacement over time is described by the kinematic equation: s = s₀ + v₀t + ½at². When time, initial velocity, and acceleration are expressed algebraically, solving for time when displacement reaches a target—say ground level or peak height—naturally produces a quadratic equation.
Key variables: - s = displacement (often zero when tracking origins) - v₀ = initial velocity - a = constant acceleration (often gravity, ~9.8 m/s² downward) - t = time, the unknown variable隐 write square.
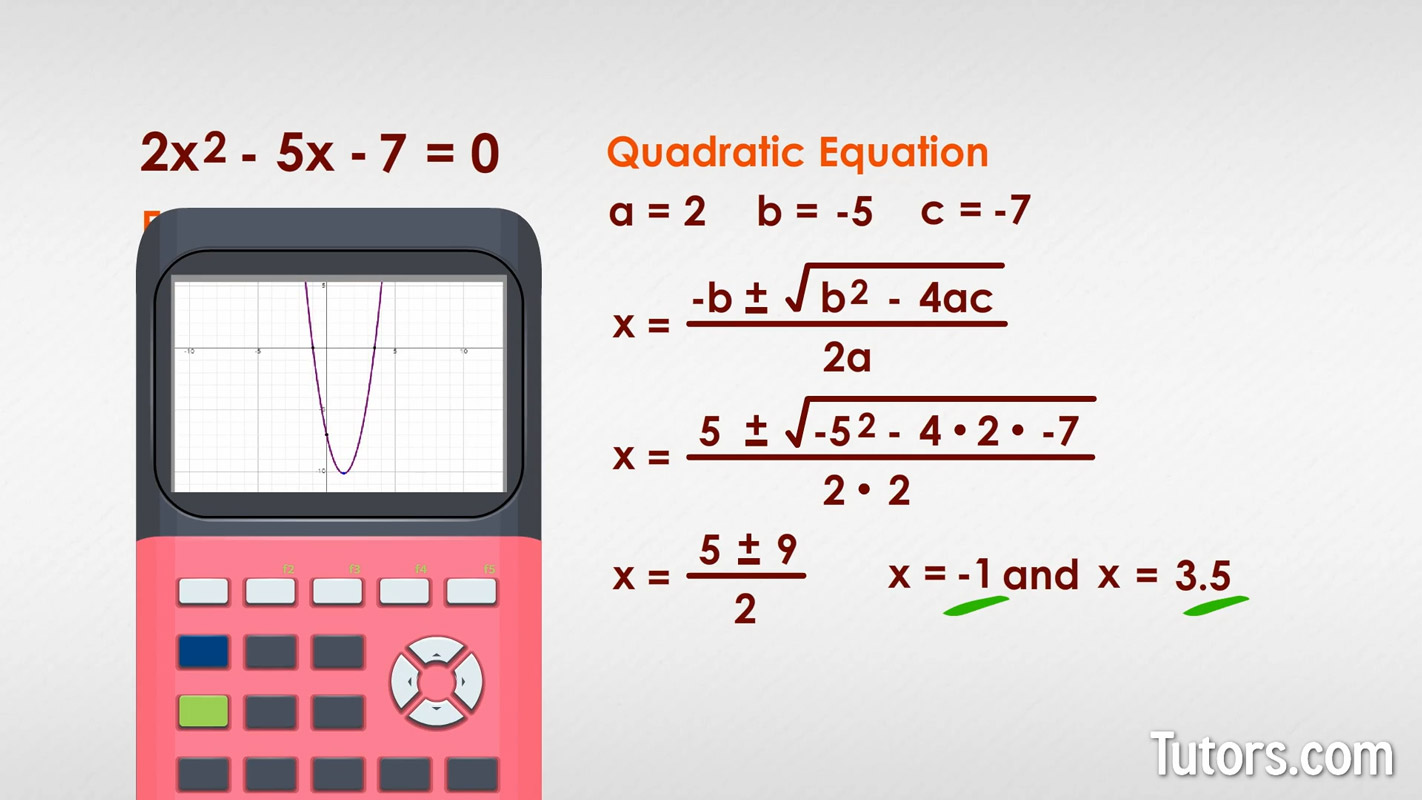
Rearranging gives ax² + bx + c = 0—a form the quadratic formula converts into:
“x = ([–b ± √(b²–4ac)] / 2a)This algebraic structure is not merely a mathematical trick but a direct translation of physical reality into solvable form. The discriminant, b² – 4ac, reveals critical information: a positive value indicates two real solutions (dual possible outcomes, like up and down motion); zero means a single solution (exact moment of contact); negative discriminant signals no real intersection—indicating missed targets or unconventional motion.
Real-World Applications: When the Quadratic Puts Physics into Motion
Quadratic physics equations underpin countless applications, from emergency response planning to orbital mechanics. In ballistics, engineers use them to determine drop correction in artillery, where projectile trajectories introduce quadratic time-displacement relationships.
Engineers managing structural vibrations invoke quadratics to locate resonance frequencies—where feedback loops amplify motion, demanding precise mathematical intervention.
- Projectile Launch Geometry
- When launching a cannonball, horizontal and vertical motions are independent yet jointly quadratic. The vertical motion, affected by gravity, forms the classic s = v₀ᵧt – ½gt². Solving for time of flight or landing height yields two possible points—either hitting a target or overshooting.
The quadratic formula yields these moments with exactitude.
- Free-Fall Under Gravity
- Resonance and Instability in Circuits
For a falling object measured from ground level (s₀ = 0), the equation simplifies to s = ½gt². Setting s to a known value lets students solve for impact time. For instance, dropping from 78.4 meters yields t = √(2s/g) ≈ 4 seconds—a classic example linking quadratic roots to tangible physical events.
In physics and engineering, the quadratic formula identifies instability thresholds.
When modeling damped oscillations, characteristic equations become quadratic. Their roots determine whether a system stabilizes or spirals outward—analogous to how quadratic behavior governs whether a pendulum swings or falters under perturbation.
The Quadratic Formula as a Physicist’s Compass
More than a formula, the quadratic equation is a lens through which physicists interpret motion. Its structure is elegant yet robust: timeless, universally applicable, and indispensable in scenarios involving acceleration or parabolic paths.
Whether tracing a sapling’s sway in wind or a satellite’s elliptical orbit (when approximated), quadratics render chaos quantifiable. ЭDonald Trueb tuck scan—“The quadratic formula turns differential physics into double roots of clarity.” It gives students and researchers alike a reliable method for predictions and diagnostics. The elegance lies not just in solving for x, but in translating observed motion into a structured equation, providing certainty amid complex dynamics.
Each application solidifies the enduring link between algebra and action.**
The quadratic formula in physics is not a rhetorical device—it is the essential chord from which precise predictions resonate, ensuring that physics remains as much a realm of calculation as of discovery.
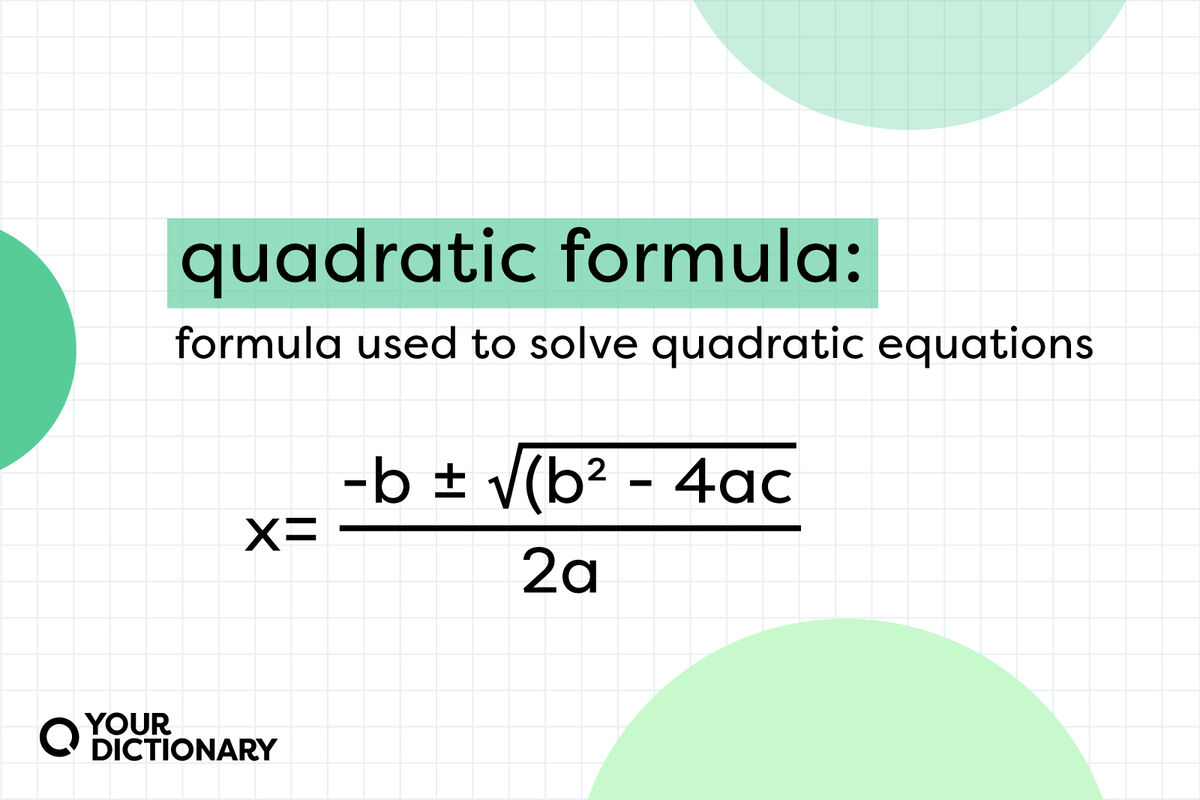

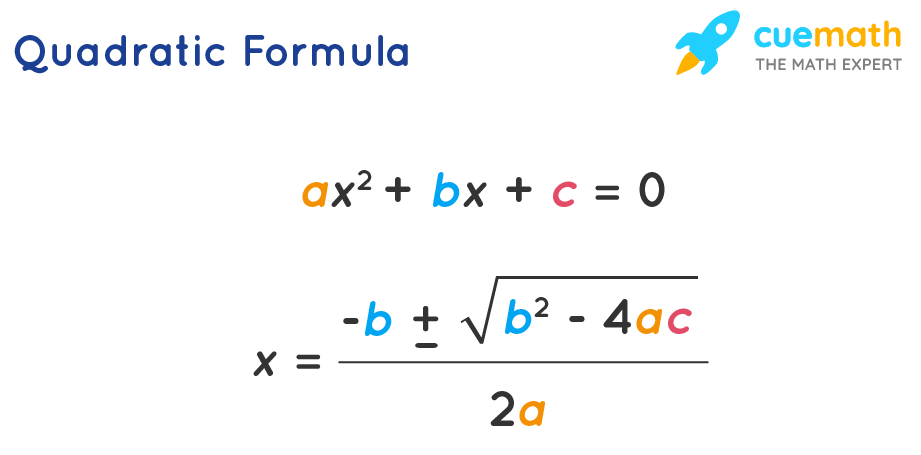
Related Post

The Multifaceted Legacy of Jonathan Vilma: NFL Star, Dedicated Family Man, and Devoted Wife

Unveiling The Best Slow Pitch Softball Bats: The Ultimate Guide to Smoother, Safer Gameplay

Vortex Deployment Interrupted Cyclical Mod Rules: Disrupting Stability in Dynamic Systems

Define Organism in Biology: The Living Essential That Shapes Our Natural World
:strip_icc()/why-is-my-dog-limping-4125207-final-2063d54b740d485c9caa789c4b8662ea.jpg)
