Unlocking the Physics of Impact: How the Elastic Collision Equation Shapes Our Understanding of Collisions

When two masses meet in a sudden, forceful encounter—whether in a sport, a scientific experiment, or a theoretical model—the dynamics of energy and momentum dictate the outcome. At the heart of this interaction lies the Elastic Collision Equation, a precise mathematical framework that describes how kinetic energy and momentum are preserved during perfectly elastic collisions. This principle, deeply rooted in classical mechanics, enables engineers, physicists, and designers to predict particle behavior, optimize safety systems, and simulate complex physical systems with remarkable accuracy.

From particle accelerators to billiard balls rolling across a table, understanding this equation is essential to unlocking the behavior of colliding bodies.

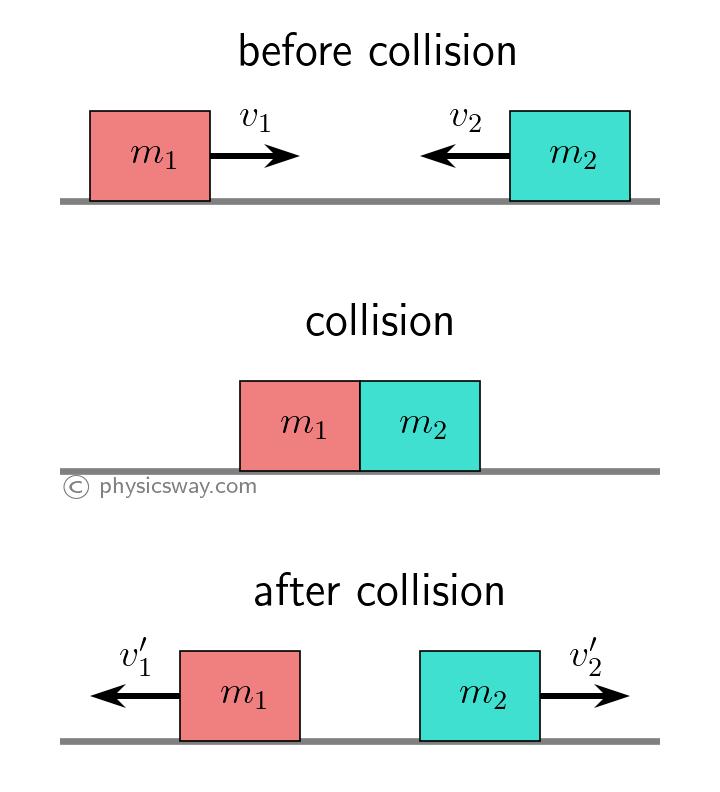
The Elastic Collision Equation applies specifically to interactions governed by two fundamental conservation laws: conservation of momentum and conservation of kinetic energy. Unlike inelastic collisions, where some kinetic energy transforms into heat or sound, elastic collisions maintain total momentum and total kinetic energy before and after contact.

This distinction is critical — it defines a system’s elasticity, a property vital in fields ranging from aerospace engineering to biomechanics.

“Elastic collisions represent the idealized boundary of interaction: perfectly energy-conserving, informing both theoretical models and real-world design.” —Dr. Elena Marquez, applied physicist specializing in collision dynamics

Mathematically, for a one-dimensional collision between two particles, the Elastic Collision Equations are:

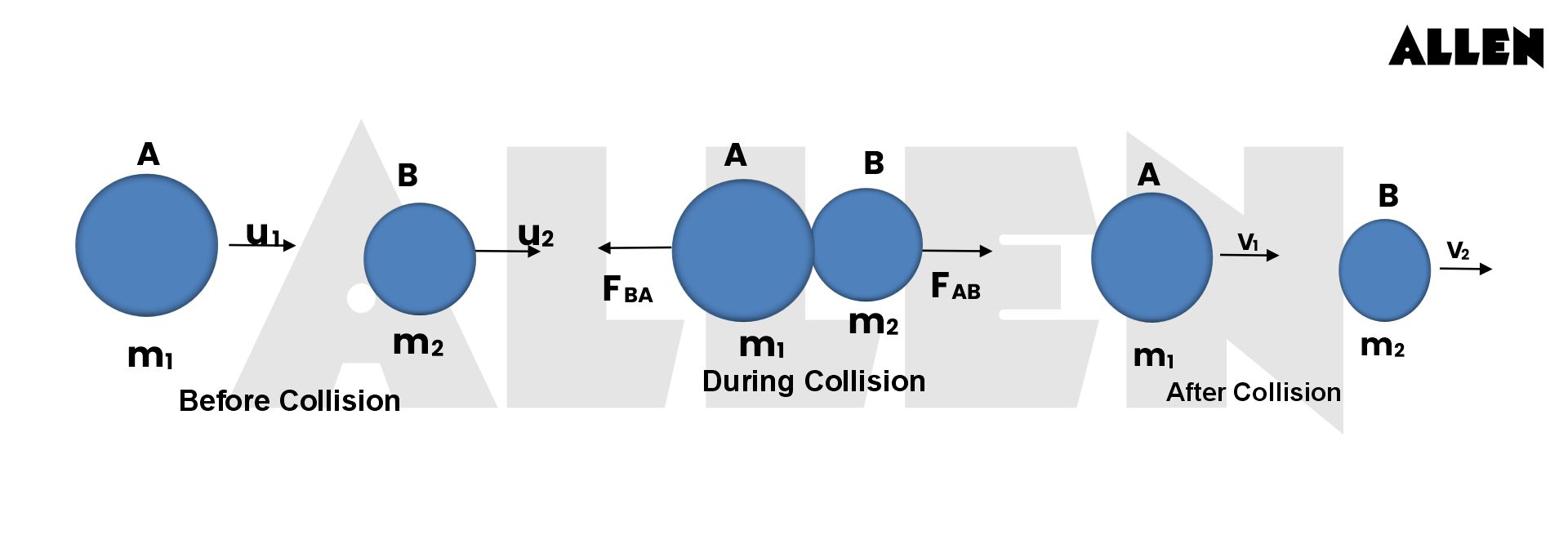
Conservation of Momentum: m₁v₁ᵢ + m₂v₂ᵢ = m₁v₁f + m₂v₂f

Conservation of Kinetic Energy: ½m₁v₁ᵢ² + ½m₂v₂ᵢ² = ½m₁v₁f² + ½m₂v₂f²

Where m₁ and m₂ denote the masses, v₁ᵢ and v₂ᵢ are initial velocities, and v₁f and v₂f represent final velocities. Solving these simultaneously yields final velocities:

Final Velocity of Particle 1: v₁f = [(m₁ – m₂)v₁ᵢ + 2m₂v₂ᵢ] / (m₁ + m₂)

Final Velocity of Particle 2: v₂f = [2m₁v₁ᵢ + (m₂ – m₁)v₂ᵢ] / (m₁ + m₂)

These equations form the backbone of collision analysis, applicable across vastly different scales—from atomic particles in high-energy physics to the precise impact modeling of automotive safety systems.

The Elastic vs. Inelastic Divide: A Matter of Energy Conservation

In a truly elastic event, kinetic energy remains unchanged—a hallmark distinguishing it from inelastic collisions, where energy disperses irreversibly. Consider a standard free-market of impact: in an elastic interaction, the total energy output upon separation matches the input, allowing for near-perfect reversibility in theory.

Real-world examples include,"

1. ne Git gears vibrating minimally after short collisions, dramatically reducing wear
2. ra ball bearings in precision machinery that maintain predictable motion with negligible energy loss
3. sports like volleyball, where controlled rebound depends on minimal energy dissipation

Engineers leverage this principle when designing high-efficiency systems—such as centrifugal pumps or turbine blades—where preserving kinetic energy minimizes waste and enhances performance.

Engineering Applications: From Microscopes to Machinery

The Elastic Collision Equation is far more than academic theory; it drives innovation in design and simulation. In particle physics, where subatomic particles collide at near light speeds, elastic models guide detector calibration and theoretical predictions.

In automotive safety, crash simulations use these equations to anticipate energy distribution, informing crumple zone design and airbag deployment timelines.

Even in everyday objects, this principle plays a silent yet pivotal role: the gentle but precise transfer of momentum in a simulated billiard table allows gameplay realism, while still-life painters rely on collision models to replicate the subtle dynamics of falling objects. Advanced video game engines, too, utilize simplified elastic collision algorithms to simulate void interactions, enhancing realism without sacrificing performance.

Limitations and Idealization: Navigating the Real-World Nuance

“While the elastic model offers ideal clarity, real-world materials absorb energy through deformation, heat, or vibration—revealing that ‘perfect elasticity’ exists on a spectrum.”

No physical system achieves true elasticity due to internal material damping, surface friction, and microscopic dissolution. Even steel or perfectly rigid synthetic materials exhibit minute energy loss.

Engineers account for this through correction factors and empirical testing, blending theory with real-world measurement. This calibration ensures simulations closely mirror physical behavior, bridging the gap between ideal and practical outcomes.

The Future of Collision Modeling: Enhanced Precision via Computational Advances

Emerging computational techniques—such as finite element analysis and machine learning-driven simulations—are expanding the reach of the Elastic Collision Equation. These tools integrate multi-body systems, variable material properties, and complex boundary conditions far beyond classical two-body treatments.

By combining these models with empirical data, researchers simulate increasingly realistic scenarios, from microscale device mechanics to large-scale astrophysical interactions.

Furthermore, advancements in nanotechnology are probing elasticity at atomic scales, revealing how quantum effects challenge traditional macroscopic assumptions. In these realms, collision dynamics begin integrating elastic principles with quantum scattering laws, pushing the boundaries of classical physics.

The Elastic Collision Equation, though rooted in 18th-century mechanics via Newton and Leibniz, remains a living cornerstone of modern science and engineering. Its role in balancing simplicity and predictive power ensures continued relevance across disciplines, guiding innovation while honoring foundational physical truths.

As technology evolves, so too does the application of this elegant principle—transforming abstract equations into real-world impact, one collision at a time.