Unlocking Trigonometric Mysteries: How Trig Half-Angle Identities Revolutionize Half-Angle Computations

For centuries, trigonometric challenges involving angle halves—once cumbersome and error-prone—have found clarity through a powerful set of identities: the trig half-angle formulas. These algebraic tools transform complex expressions involving angles like θ/2 into manageable components recast in terms of sin θ, cos θ, or tan θ, enabling precise calculations in engineering, physics, and computer graphics. Far more than mere shortcuts, the half-angle identities serve as foundational keys unlocking deeper understanding of periodic functions and dynamic systems.

The Core Mechanism: Deriving Trig Half-Angle Identities from the Power of Twice

At their heart, trig half-angle identities emerge from squaring the double-angle formulas—a insight that reveals elegant symmetries beneath trigonometric expressions.

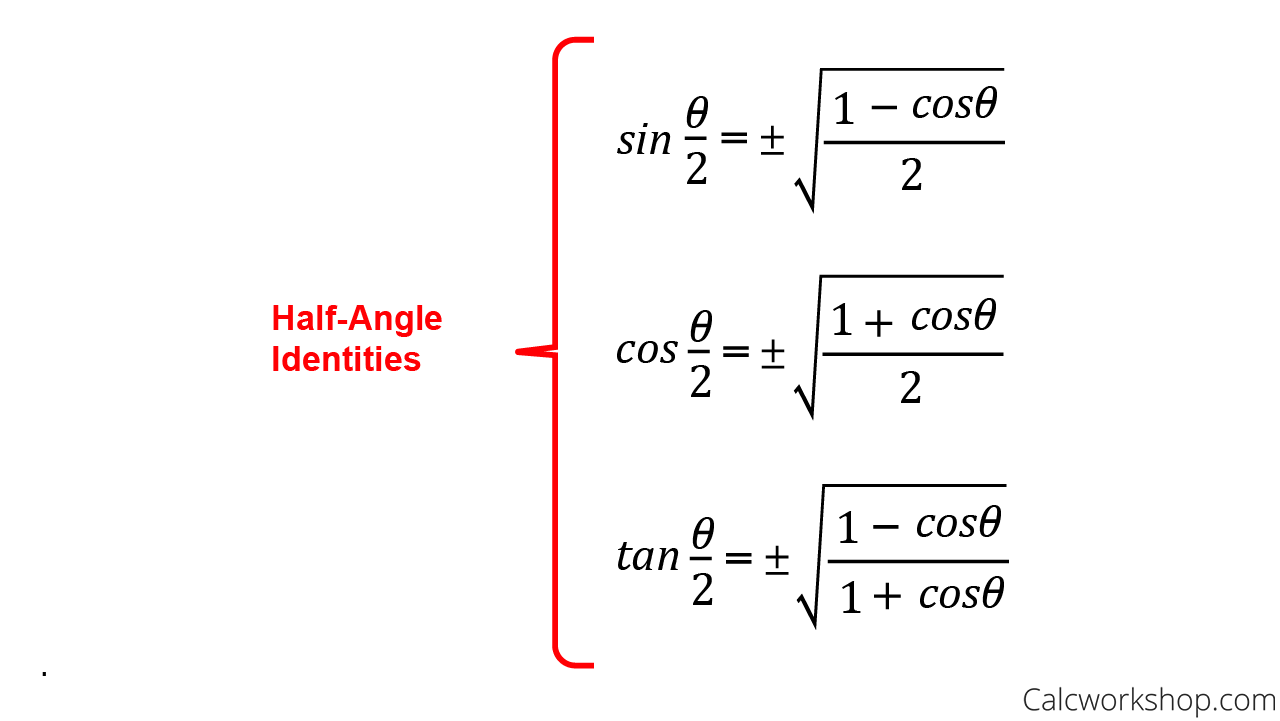
These identities allow direct translation of problems involving half-angles into forms directly tied to the original angle, simplifying integration, differentiation, and equation solving. The key insight: when θ = α/2, the half-angle identities express sin(α/2), cos(α/2), and tan(α/2) purely in terms of sin α, cos α, or tan α, unlocking computational pathways once shrouded in complexity. The standard identities are as follows:

• For sine: sin(α/2) = ±√[(1 – cos α)/2]
• For cosine: cos(α/2) = ±√[(1 + cos α)/2]
• For tangent: tan(α/2) = ±√[(1 – cos α)/(1 + cos α)] = (1 – cos α)/sin α

Each expression, rooted in Pythagorean fundamentals and derived from algebraic manipulation of double-angle formulas, enables engineers and mathematicians to decode periodic behaviors with precision.

The ± sign, determined by α’s quadrant, ensures correct sign propagation—critical in real-world applications where direction and phase matter.

From Formulas to Applications: Engineering and Computing in Action

Trig half-angle identities are not just theoretical constructs—they power innovation across disciplines. In electrical engineering, AC circuit analysis relies on half-angle identities to model phase shifts in power transmission, ensuring efficient grid operation. In signal processing, Fourier transforms leverage these identities to decompose complex waveforms into fundamental sine and cosine components, bridging time and frequency domains.

Computer graphics and animation depend on precise rotation and scaling, tasks where half-angle identities streamline rotations around arbitrary axes.

In physics, angular momentum calculations and pendulum motion modeling often reduce to half-angle expressions, turning abstract dynamics into quantifiable predictions. “These identities are silent workhorses in computational systems,” notes Dr. Elena Torres, a researcher at the Institute for Applied Mathematics.

“They convert recursive angle doubling into direct forward step-by-step evaluation—dramatically reducing floating-point error over iterations.”

In structural engineering, half-angle formulas assist in analyzing forces at midpoints of beams, where load distributions hinge on angle bisectors and rotational symmetry—both naturally expressed through half-angle trigonometry.

Computational Advantages and Algorithmic Efficiency

The real power of half-angle identities shines in computational environments. Direct evaluation avoids costly iterative methods or recursive doubling, accelerating algorithms essential for real-time simulations and rapid prototyping. Consider a drone navigation system updating orientation every 10 milliseconds: each half-angle calculation, simplified by π/2 trig reductions, supports faster control decisions without sacrificing accuracy.

For numerical solvers, the identities enable stable iterative schemes, particularly in root-finding algorithms for transcendental equations involving trig functions.

The reduced form δθ = θ/2 shortens convergence paths, minimizing oscillatory divergence common in untransformed angular calculations.

Pedagogical Value: Building Trigonometric Intuition

Learning trig half-angle identities deepens students’ grasp of trigonometric structures. Rather than memorizing isolated formulas, students uncover the intrinsic symmetry of trigonometric functions—where halves of an angle are not abstract additions but calculated descendants of the full angle’s geometry. This fosters intuitive mastery, enabling students to manipulate expressions with agility and insight.

Breaking down derivations step-by-step reveals common patterns: algebraic substitution rooted in sin²θ + cos²θ = 1, clever factoring, and disciplined handling of sign restrictions.

“Students who internalize these identities don’t just compute—they understand the ‘why’ behind the ‘how,’” observes Dr. Miriam Chen, trigonometry curriculum design expert. This conceptual firmness proves invaluable when applying trig in higher mathematics and applied fields.

Common Pitfalls and Best Practices

Despite their utility, half-angle identities often confuse beginners.

A frequent error arises from neglecting the ± sign based on α’s quadrant—an oversight that distorts results in applications like physics simulations or control systems. Equally, misapplying identities outside the domain where cos α ≠ ±1 prevents valid square roots, triggering erroneous calculations. Best Practices:

• Always identify the quadrant before choosing the sign in √[(1 ± cos α)/2].
• Use tangent identities only when numerator and denominator maintain sign consistency across intervals.
• Verify domain restrictions to avoid complex number capture in real-valued contexts.

Tools such as trigonometric tables and symbolic algebra software (e.g., Mathematica, Maple) assist professionals—but deep comprehension ensures correct interpretation and avoids overreliance on automation.

From ancient geometric origins to modern computational engines, trig half-angle identities exemplify how a single mathematical principle can bridge centuries of discovery and innovation.

Their precise, efficient restructuring of half-angles empowers both theoretical insight and practical application, making them indispensable across science and technology. Mastery of these identities transforms trigonometry from a series of puzzles into a transparent language of change, phase, and motion.

The Endless Utility of Half-Angle Insight

As technology accelerates and data demands precision, the trig half-angle identities remain steadfast: concise, robust, and deeply relevant. Whether optimizing rendering algorithms, analyzing quantum states, or designing resilient infrastructure, these identities deliver clarity in complexity.

Their elegance lies not just in solution finding, but in revealing the hidden order within trigonometric behavior—one angle at a time.