Unlocking Trigonometric Precision: The Power of Calc 2 Trig Identities in Modern Computation
Unlocking Trigonometric Precision: The Power of Calc 2 Trig Identities in Modern Computation
Calcul 2 trigonometric identities are far more than abstract formulas—they are the backbone of computational accuracy across engineering, physics, data science, and digital design. These identities, refined over centuries, provide a systematic toolkit for simplifying complex trigonometric expressions, solving equations efficiently, and strengthening numerical models. From simplifying waveforms in signal processing to stabilizing satellite trajectories and rendering 3D graphics, mastery of Calc 2 trig identities enables professionals to transform nebulous angular relationships into actionable, precise results.
Their enduring value lies in their dual role: elegant mathematical theory and practical engineering utility.
At the heart of trigonometric analysis are the foundational Calc 2 identity families: Pythagorean, reciprocal, quotient, and even co-function relationships. These identities act as transformation rules, allowing multifaceted expressions into equivalent forms that reveal hidden patterns.
For example, recognizing that $\cos^2\theta = 1 - \sin^2\theta$ permits substitution during integration, while the identity $\sec\theta = \frac{1}{\cos\theta}$ streamlines differentiation—critical steps when modeling periodic phenomena. These tools don’t just simplify calculations; they unlock deeper insight into the cyclical nature of trigonometric functions.
Core Identity Families and Their Computational Roles
The four primary Calc 2 trigonometric identities form distinct yet interconnected categories, each serving a unique purpose in transformational problem-solving: **1. Pythagorean Identities** – Derived directly from the Pythagorean theorem, these identities anchor trigonometric manipulation.- $\sin^2\theta + \cos^2\theta = 1$ allows substitution of $\sin^2\theta$ for $1 - \cos^2\theta$ and vice versa. - $1 + \tan^2\theta = \sec^2\theta$ and $\cot^2\theta + 1 = \csc^2\theta$ offer rapid conversion between tangent, cotangent, secant, and cosecant, vital in vector projections and AC circuit analysis. **2.
Reciprocal Identities** – These express fundamental functions in inverted form, essential for normalizing expressions: - $\csc\theta = \frac{1}{\sin\theta}$, $\sec\theta = \frac{1}{\cos\theta}$, $\cot\theta = \frac{1}{\tan\theta}$. - Though seemingly straightforward, their proper use avoids sign errors and facilitates simplification in integrals involving rational trigonometric forms. **3.
Quotient Identities** – These relate tangent and cotangent to sine and cosine, enabling angle reduction: - $\tan\theta = \frac{\sin\theta}{\cos\theta}$, $\cot\theta = \frac{\cos\theta}{\sin\theta}$. - In computational physics, they convert steep slope evaluations into ratio-based computations, improving numerical stability. **4.
Co-Function Identities** – These exploit symmetry in the unit circle, revealing functional complementarity: - $\sin(\frac{\pi}{2} - \theta) = \cos\theta$, $\cos(\frac{\pi}{2} - \theta) = \sin\theta$, - $\tan(\frac{\pi}{2} - \theta) = \cot\theta$. - Critical in angular transformation, especially when rotating coordinate systems or analyzing wave interference patterns. Understanding these categories empowers analysts to navigate trigonometric

![Trig Identities Derivatives [Inverse, Antiderivative]](https://trigidentities.net/wp-content/uploads/2022/10/Antiderivative-Trig-Identities.jpg)
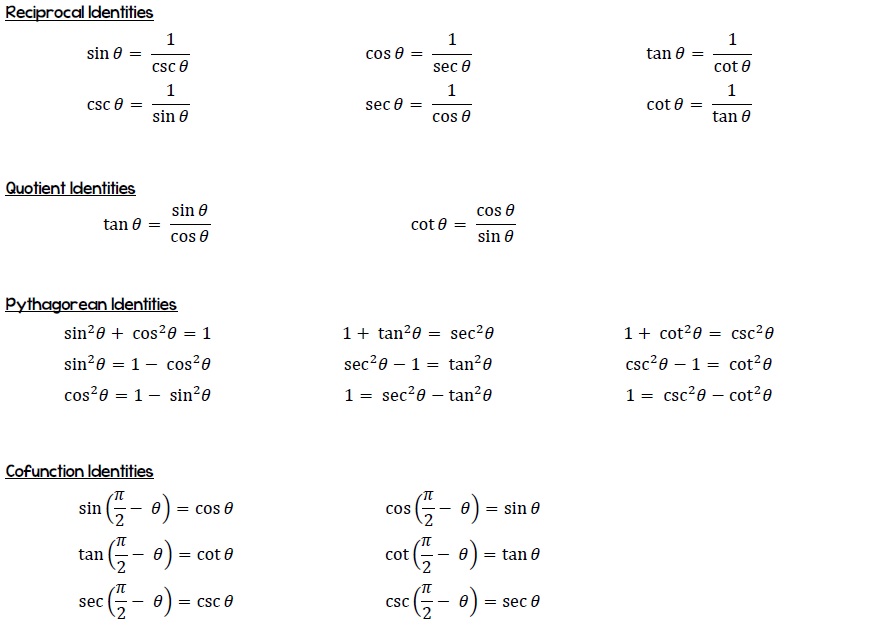
Related Post

Stay Ahead: Northfield Schools News Delivers What Matters, When You Need It

Sandra Smith Fox Salary: The Data That Redefines Expected Earnings in Modern Professionals

Rodrygos Dribbling Mastery A Season In Review: The Player Who Redefined Flair on the Pitch

E Learning UFL: Seasonal Prime? Spring Learning University of Florida’s Digital Promise

