Unveiling the Power of Binomial Expansion: How a Single Formula Powers Modern Mathematics
Unveiling the Power of Binomial Expansion: How a Single Formula Powers Modern Mathematics
At the heart of algebraic computation lies a deceptively simple yet infinitely profound formula—the Binomial Expansion Formula—that transforms the mysterious expansion of powers of binomials into a structured, predictable process. From simplifying complex expressions to enabling approximations critical in engineering and statistics, this mathematical tool turns effortful manual expansion into systematic calculation. Using the Binomial Expansion Formula, mathematicians and scientists unlock precise coefficients that govern polynomial growth, probability distributions, and even machine learning algorithms.
Its simplicity masks a transformative role that touches disciplines far beyond classical algebra.
The Binomial Expansion Formula: A Mathematical Cornerstone
The Binomial Expansion Formula describes how to expand expressions of the form $(a + b)^n$ where $n$ is any non-negative integer. Mathematically expressed, it states: $$(a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k$$ where $\binom{n}{k} = \frac{n!}{k!(n-k)!}$ is the binomial coefficient, representing the number of ways to choose $k$ elements from $n$. This formula generalizes intuitive logic into a universal expansion rule applicable to any whole-number exponent.
Its elegance lies in its ability to replace tedious term-by-term multiplication with a formula-based computation.
For example, expand $(x + 2)^5$: Using the formula, the expansion yields $$x^5 + 10x^4 \cdot 2 + 10x^3 \cdot 4 + 5x^2 \cdot 8 + 10x \cdot 16 + 32$$ which simplifies neatly to $$x^5 + 10x^4 + 40x^3 + 40x^2 + 160x + 32$$ each coefficient emerging directly from the binomial coefficients embedded in the expansion. This systematic extraction of terms reveals the formula’s true power—transforming combinatorial complexity into transparent computation.
Expanding Perspectives: The Role of Coefficients in Mathematical Modeling
Central to the Binomial Expansion Formula are the binomial coefficients $\binom{n}{k}$, which encode multiplicative structure and symmetry. These coefficients appear not only in pure algebra but in probabilistic modeling, where they define the binomial distribution—a cornerstone of statistical inference.
> “The coefficients appear everywhere—from binomial probabilities to Taylor series approximations,” notes Dr. Elena Martinez, applied mathematician at the Institute for Applied Probability. “They bridge discrete counting and continuous approximation, making binomial expansions indispensable in statistical simulations.”
The symmetry of $\binom{n}{k}$—where $\binom{n}{k} = \binom{n}{n-k}$—ensures that expansions are balanced and predictable.
Each term’s position in the expansion corresponds to a unique combinatorial choice between $a$ and $b$, reinforcing a deep connection between algebra and discrete mathematics. This symmetry enables efficient computation even for large $n$, a feature leveraged extensively in algorithms and numerical methods.
Applications Across Science and Technology
Beyond elementary expansion, the Binomial Expansion Formula drives advanced applications in diverse fields. In physics, it underpins perturbation theory, where small corrections to ideal systems are calculated using expansions.
In computer science, it powers polynomial evaluation algorithms vital for cryptography and error correction. Machine learning models often use polynomial approximations derived from binomial-like expansions to simplify complex loss surfaces, improving training efficiency.
Statisticians rely on binomial expansions when working with confidence intervals and hypothesis testing, particularly in binomial probability calculations.
“For large $n$, computing binomial probabilities term-by-term becomes infeasible,” explains Dr. Rajiv Patel, professor of mathematical statistics. “The Binomial Expansion Formula, particularly when paired with normal approximations, offers a scalable approach to statistical inference.”
Engineers applying finite element analysis and control theory also depend on these expansions to linearize nonlinear systems and solve differential equations numerically.
The formula’s reproducibility ensures consistent results across iterations—a necessity in simulation-based design and validation.
Efficiency, Precision, and Computational Scalability
One of the most compelling advantages of the Binomial Expansion Formula is computational efficiency. Instead of manually developing each term, which scales exponentially in complexity with $n$, the formula reduces expansion to a single loop across $k = 0$ to $n$. This enables high-speed evaluation even for $n > 100$, a feat foundational to fast numerical routines in software libraries like NumPy and MATLAB.
Consider high-precision arithmetic in financial modeling: where small margin changes multiply across vast portfolios, binomial expansions provide the building blocks for efficient sensitivity analysis. Similarly, in robotics, expansion formulas help approximate complex trajectory functions via polynomial fits, optimizing real-time control.
“What makes the Binomial Expansion Formula so resilient is its mathematical closure—simple, self-contained, and infinitely extendable,” says Prof.Hannah Wu, a computational algebra expert. “It’s not merely a tool but a framework for reasoning about polynomial growth and approximation.”
Challenges and Limitations in Practical Use
Despite its power, the Binomial Expansion Formula applies strictly only to integer exponents and real (or complex) bases. Extensions to fractional or negative exponents require generalized forms involving infinite series—such as the binomial series for $(1 + x)^r$, valid when $|x| < 1$.
This generalization introduces convergence considerations but remains within the formula’s conceptual umbrella, showing its conceptual durability.
Moreover, computational precision declines with large $n$, especially when coefficients grow factorially.
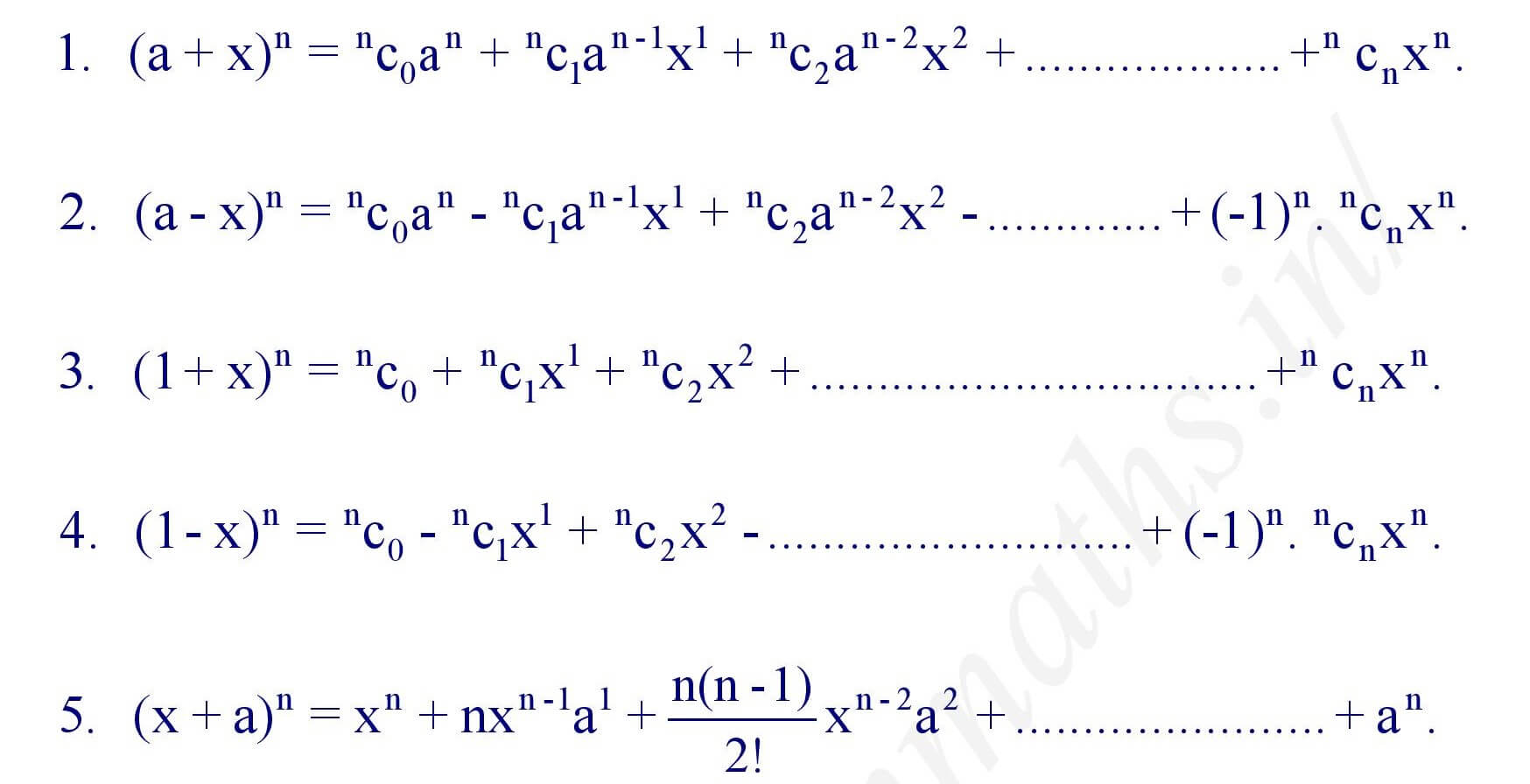



Related Post

Jamaica’s Iron Warriors Clash Today: Match & Score Predictions Ignite Caribbean Football Fever

What Type of Music Does The Weeknd Make? The Dark, Moody Sound That Defined a Generation
What Is Time in the USA Ohio? Precision in Time Zones and Daily Rhythms Across the Buckeye State

Lakland: The Hidden Engine Reshaping Modern Urban Development

